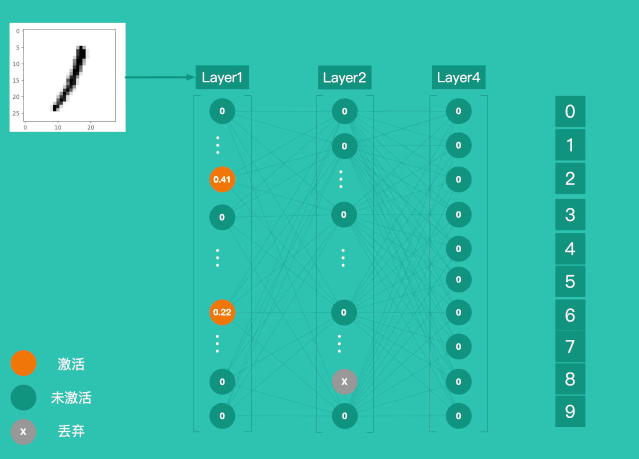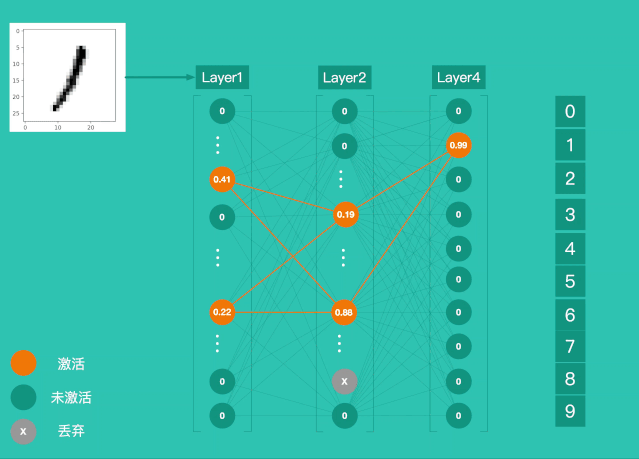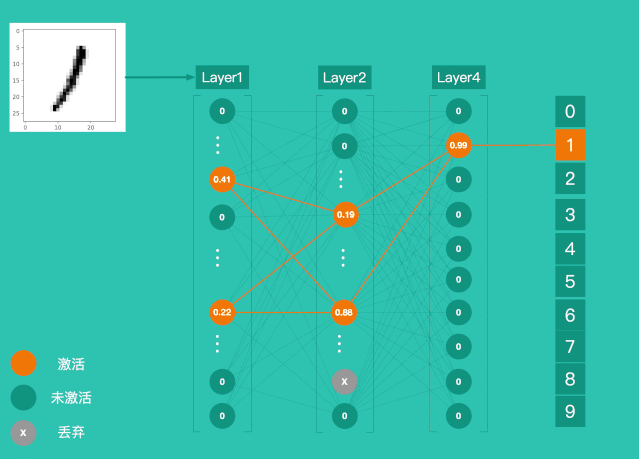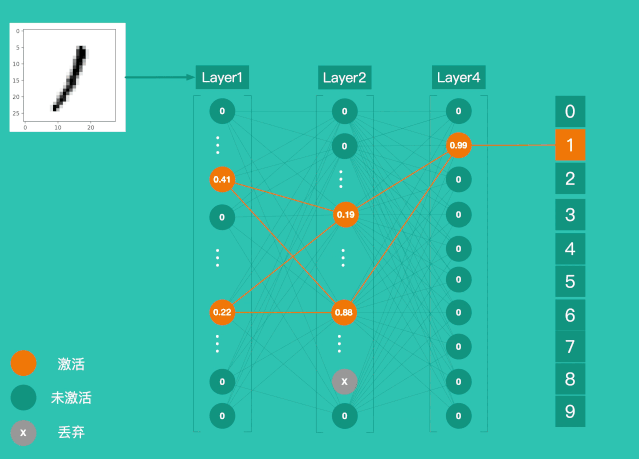
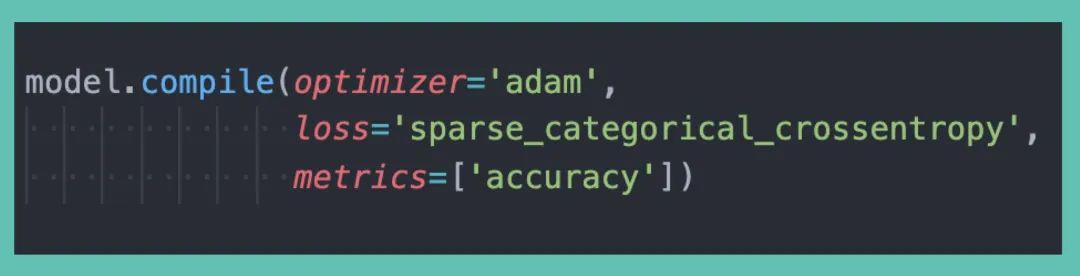
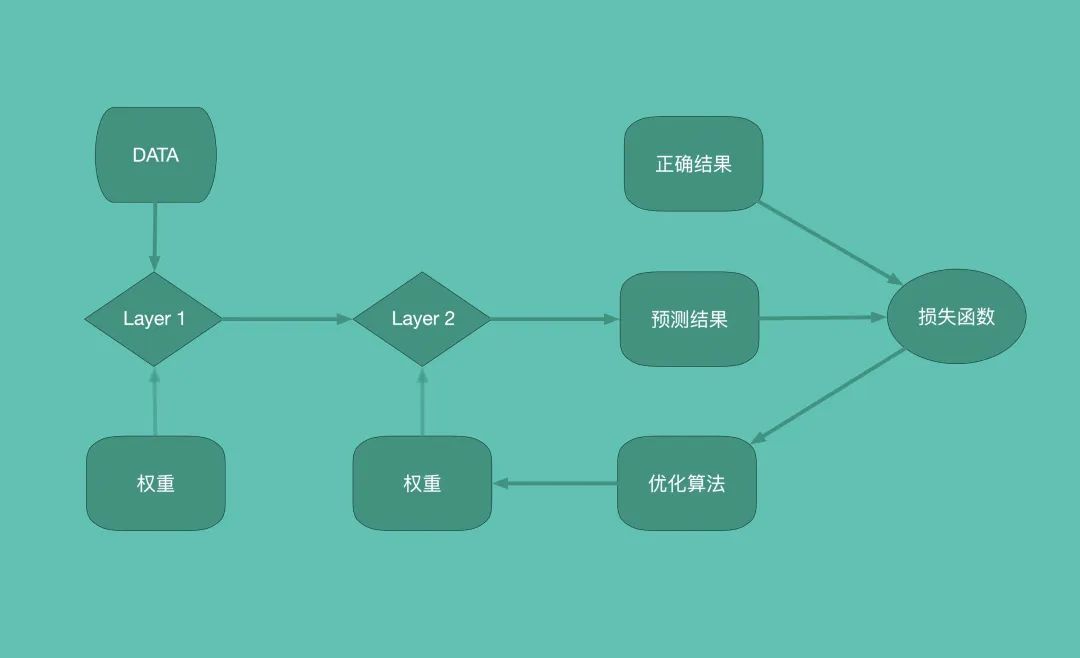
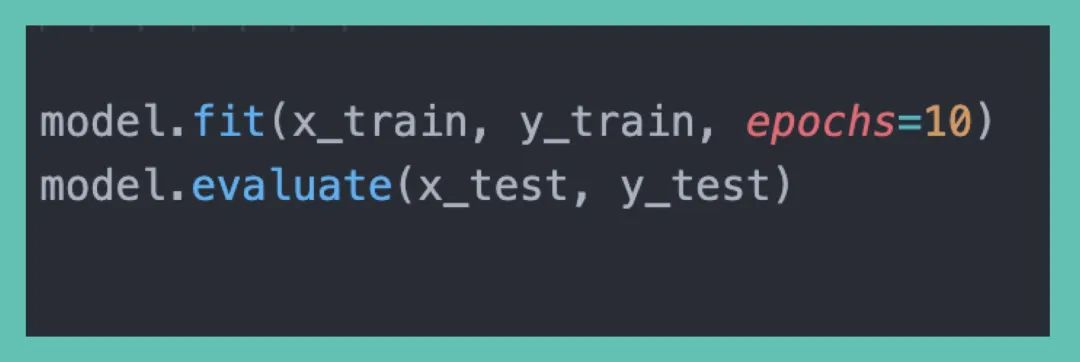
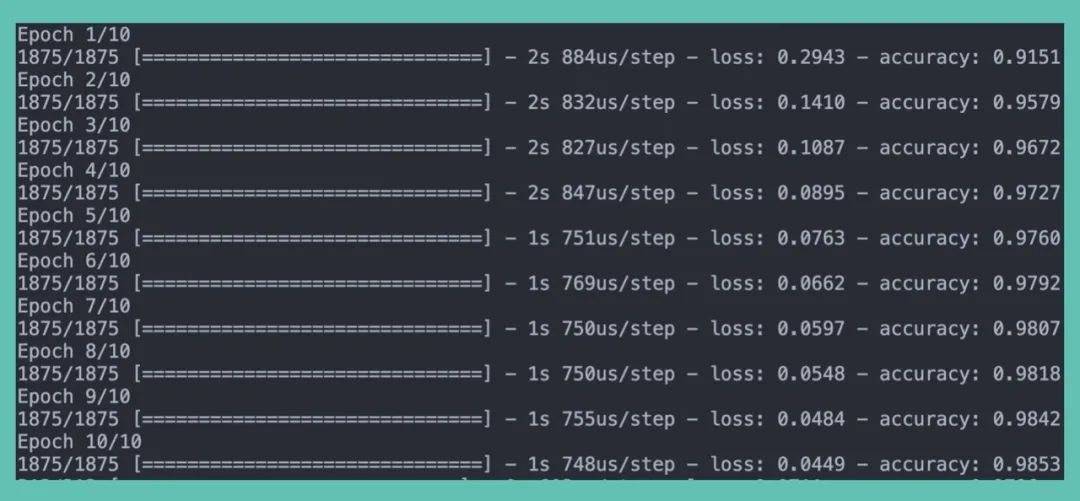
一、LPA概述
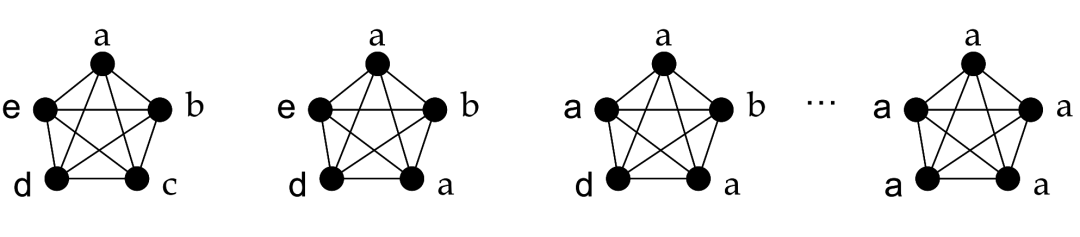
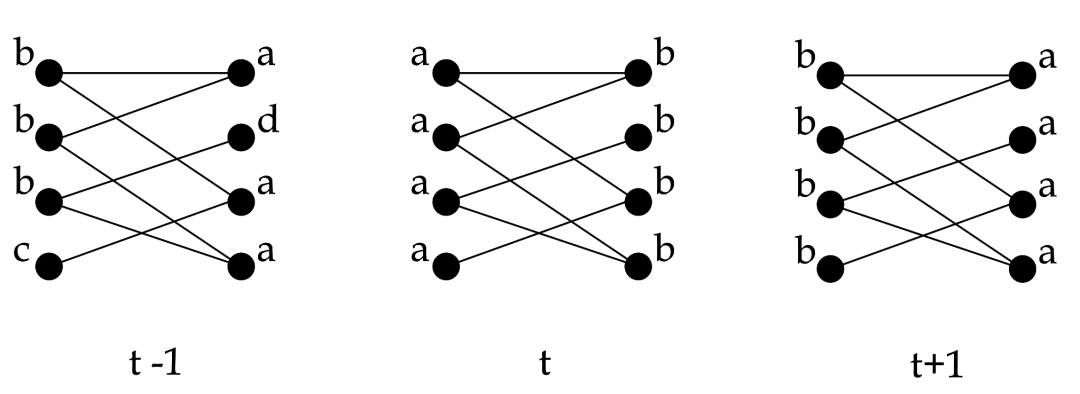
1、算法的思想
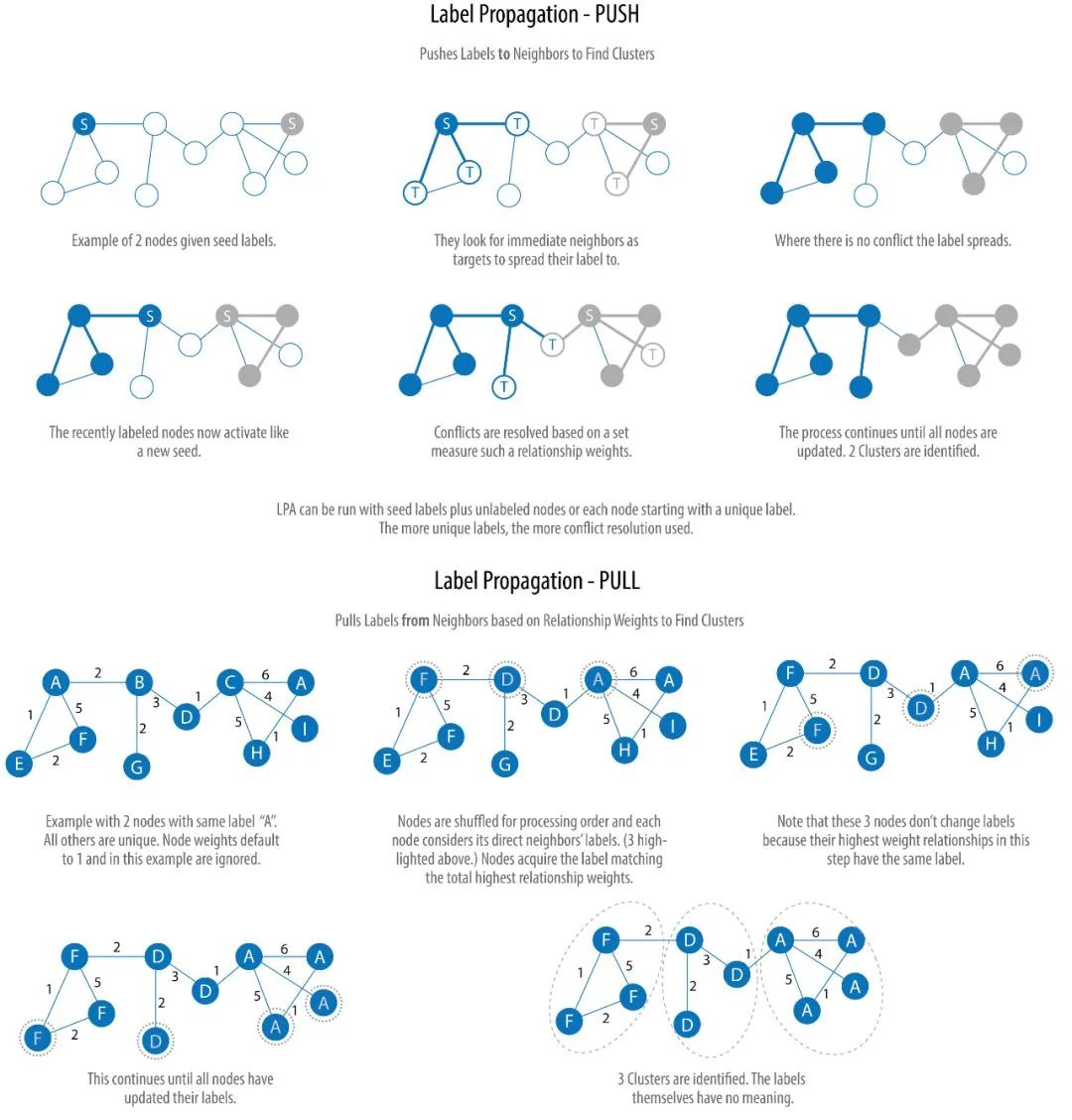
2、用于图聚类
参考原始论文 https://arxiv.org/abs/0709.2938 https://arxiv.org/pdf/0709.2938.pdf
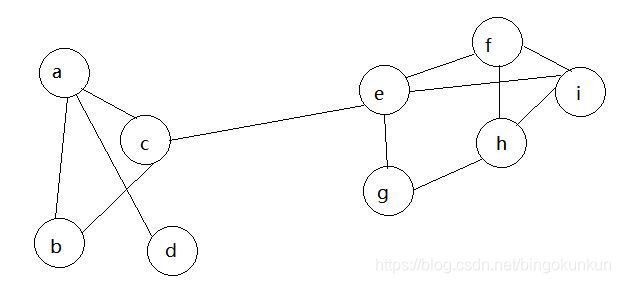

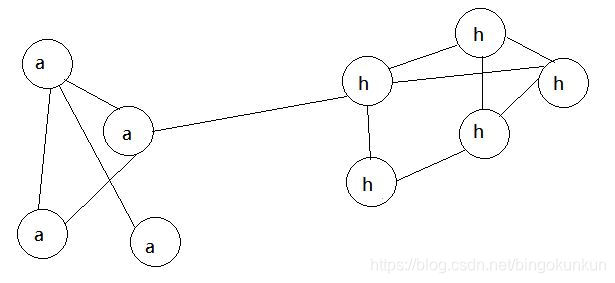
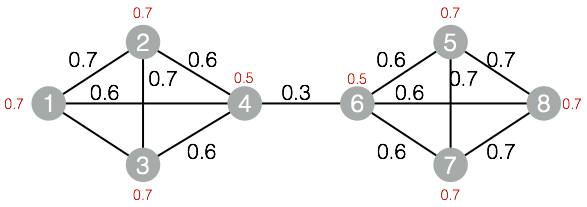
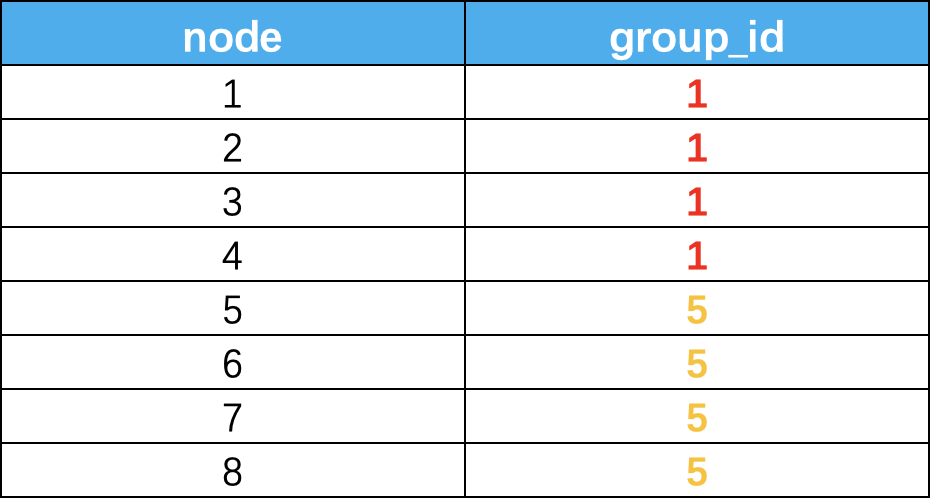
3、用于半监督
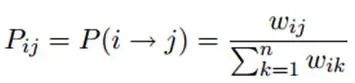
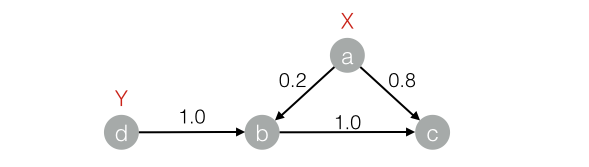
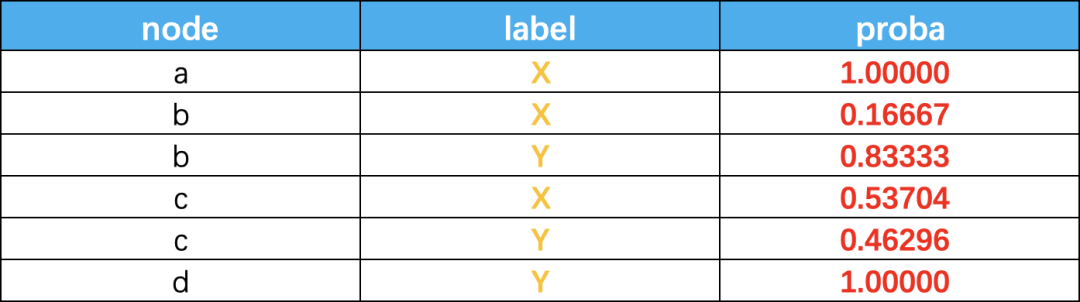
二、算法代码实现
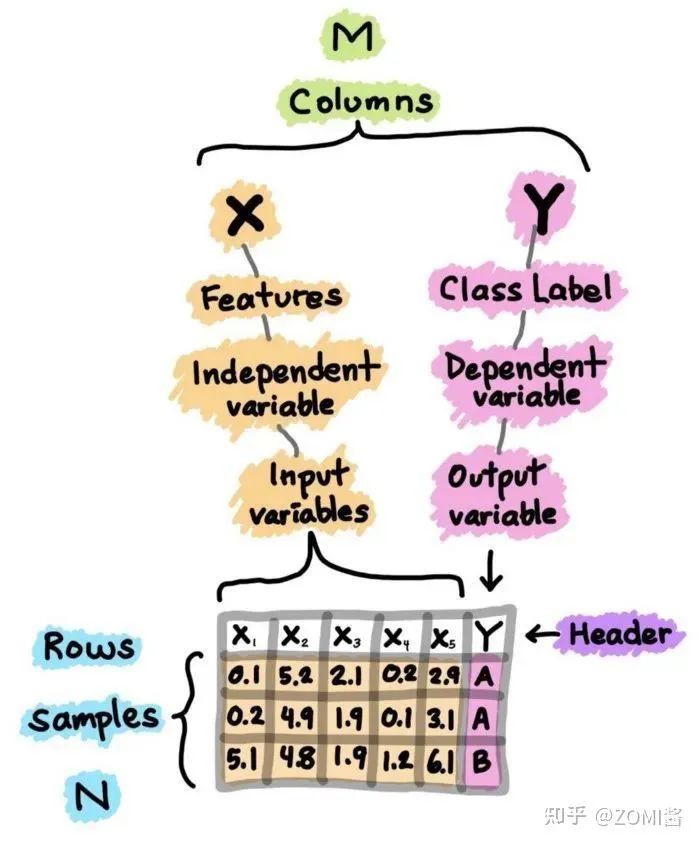
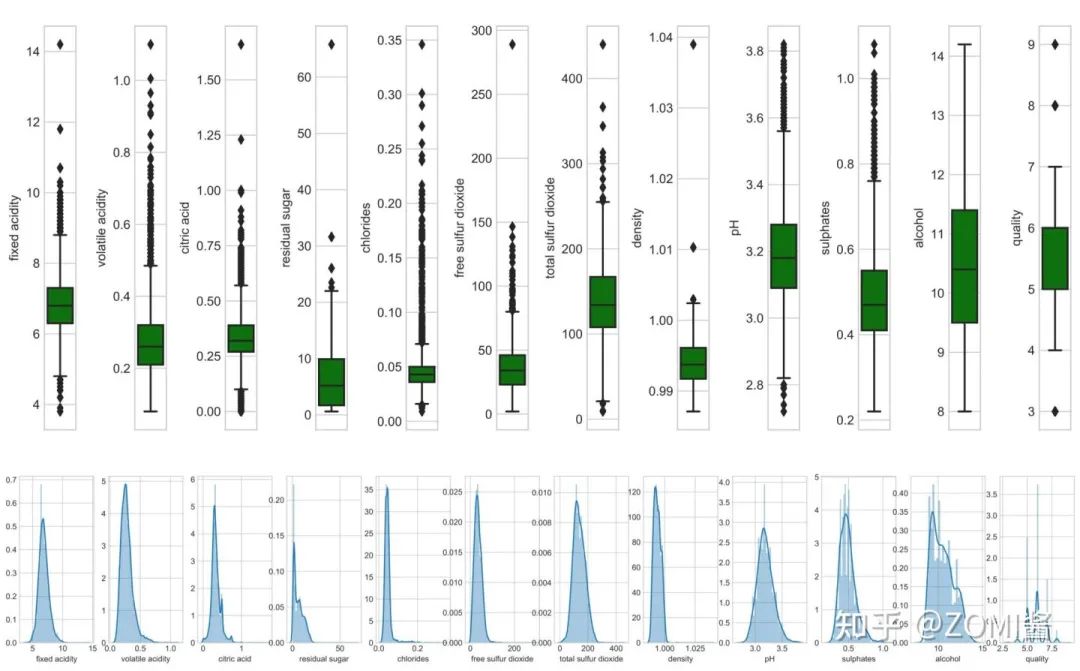
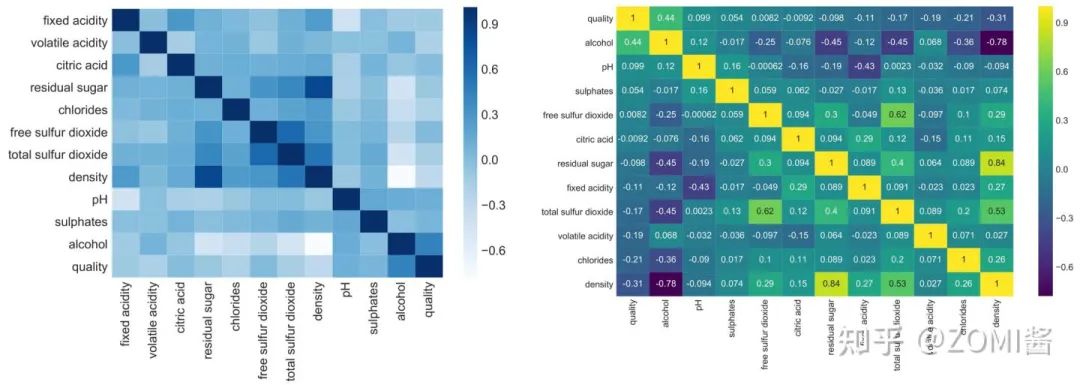
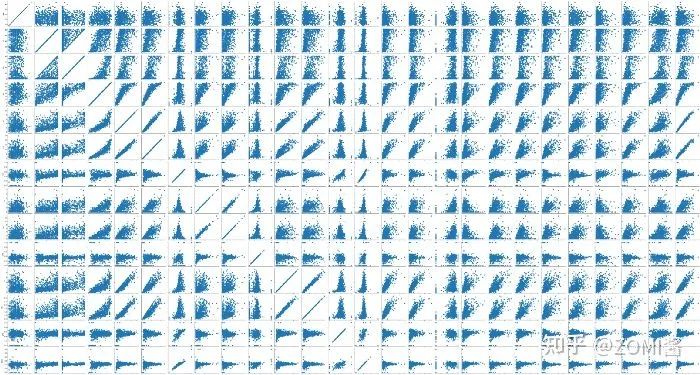
1、数据集介绍
import networkx as nxG = nx.karate_club_graph() # 空手道G.nodes()NodeView((0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33))
G.edges() EdgeView([(0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 8),(0, 10), (0, 11), (0, 12), (0, 13), (0, 17), (0, 19), (0, 21), (0, 31), (1, 2), (1, 3), (1, 7), (1, 13), (1, 17), (1, 19), (1, 21), (1, 30), (2, 3), (2, 7), (2, 8), (2, 9), (2, 13), (2, 27), (2, 28), (2, 32), (3, 7), (3, 12), (3, 13), (4, 6), (4, 10), (5, 6), (5, 10), (5, 16), (6, 16), (8, 30), (8, 32), (8, 33), (9, 33), (13, 33), (14, 32), (14, 33), (15, 32), (15, 33), (18, 32), (18, 33), (19, 33), (20, 32), (20, 33), (22, 32), (22, 33), (23, 25), (23, 27), (23, 29), (23, 32), (23, 33), (24, 25), (24, 27), (24, 31), (25, 31), (26, 29), (26, 33),(27, 33), (28, 31), (28, 33), (29, 32), (29, 33), (30, 32), (30, 33),(31, 32), (31, 33), (32, 33)])2、自己实现LPA算法
import randomimport networkx as nximport matplotlib.pyplot as plt # 应该封装成类的形式 def lpa(G): ''' 异步更新方式 G:图 return:None 通过改变节点的标签,最后通过标签来划分社区 算法终止条件:迭代次数超过设定值 ''' max_iter_num = 0 # 迭代次数 while max_iter_num < 10: max_iter_num += 1 print('迭代次数',max_iter_num) for node in G: count = {} # 记录邻居节点及其标签 for nbr in G.neighbors(node): # node的邻居节点 label = G.nodes[nbr]['labels'] count[label] = count.setdefault(label,0) + 1 #找到出现次数最多的标签 count_items = sorted(count.items(),key=lambda x:-x[-1]) best_labels = [k for k,v in count_items if v == count_items[0][1]] #当多个标签最大技术值相同时随机选取一个标签 label = random.sample(best_labels,1)[0] # 返回的是列表,所以需要[0] G.nodes[node]['labels'] = label # 更新标签 def draw_picture(G): # 画图 node_color = [float(G.nodes[v]['labels']) for v in G] pos = nx.spring_layout(G) # 节点的布局为spring型 plt.figure(figsize = (8,6)) # 图片大小 nx.draw_networkx(G,pos=pos,node_color=node_color) plt.show() if __name__ == "__main__": G = nx.karate_club_graph() #空手道数据集 # 给节点添加标签 for node in G: G.add_node(node, labels = node) #用labels的状态 lpa(G) com = set([G.nodes[node]['labels'] for node inG]) print('社区数量',len(com)) draw_picture(G)
迭代次数 1迭代次数 2迭代次数 3迭代次数 4迭代次数 5迭代次数 6迭代次数 7迭代次数 8迭代次数 9迭代次数 10社区数量 3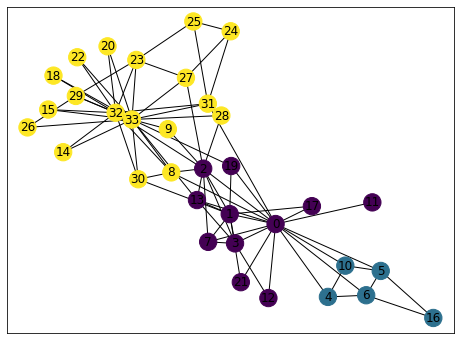
3、调包实现LPA算法
import matplotlib.pyplot as pltimport networkx as nxfrom networkx.algorithms.community import asyn_lpa_communities as lpa
# 空手道俱乐部G = nx.karate_club_graph()com = list(lpa(G))print('社区数量',len(com))
com [{0, 1, 2, 3, 7, 8, 9, 11, 12, 13, 17, 19, 21, 30},{4, 5, 6, 10, 16},{14, 15, 18, 20, 22, 23, 24, 25, 26, 27, 28, 29, 31, 32, 33}]
# 下面是画图pos = nx.spring_layout(G) # 节点的布局为spring型NodeId = list(G.nodes())node_size = [G.degree(i)**1.2*90 for i in NodeId] # 节点大小
plt.figure(figsize = (8,6)) # 设置图片大小nx.draw(G,pos, with_labels=True, node_size =node_size, node_color='w', node_shape = '.' )
'''node_size表示节点大小node_color表示节点颜色with_labels=True表示节点是否带标签'''color_list = ['pink','orange','r','g','b','y','m','gray','black','c','brown']
for i in range(len(com)): nx.draw_networkx_nodes(G, pos, nodelist=com[i], node_color = color_list[i+2], label=True)plt.show()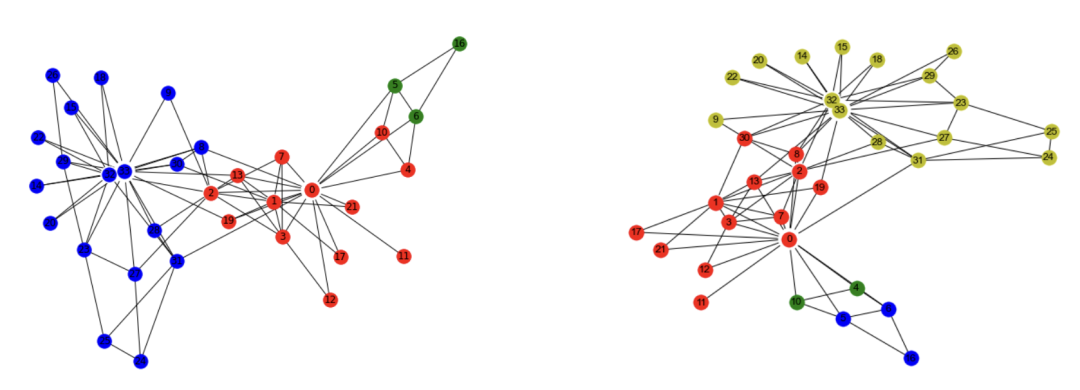
三、分群结果可视化
library('igraph')karate <- graph.famous("Zachary")community <- label.propagation.community(karate)# 计算模块度modularity(community)0.3717949
#membership查看每个点的各自分组情况。membership(community)1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 2 1 1 2 1 2 1 2 2 2 2 2 2 2 2 2 2 2 2
plot(community,karate)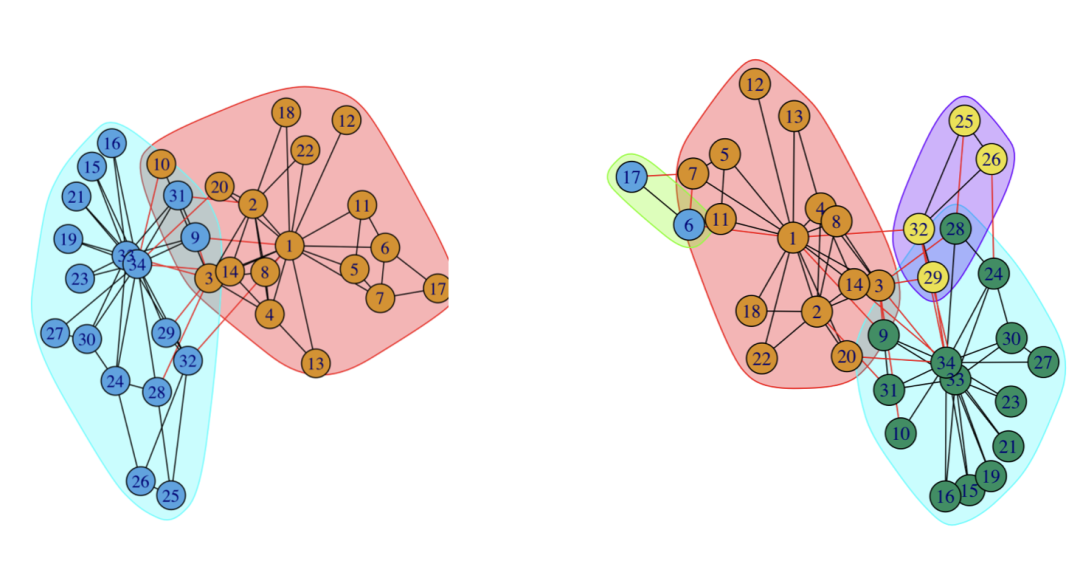
community <- walktrap.community(karate, weights = E(karate)$weight, steps = 8, merges =TRUE, modularity = TRUE)plot(community,karate)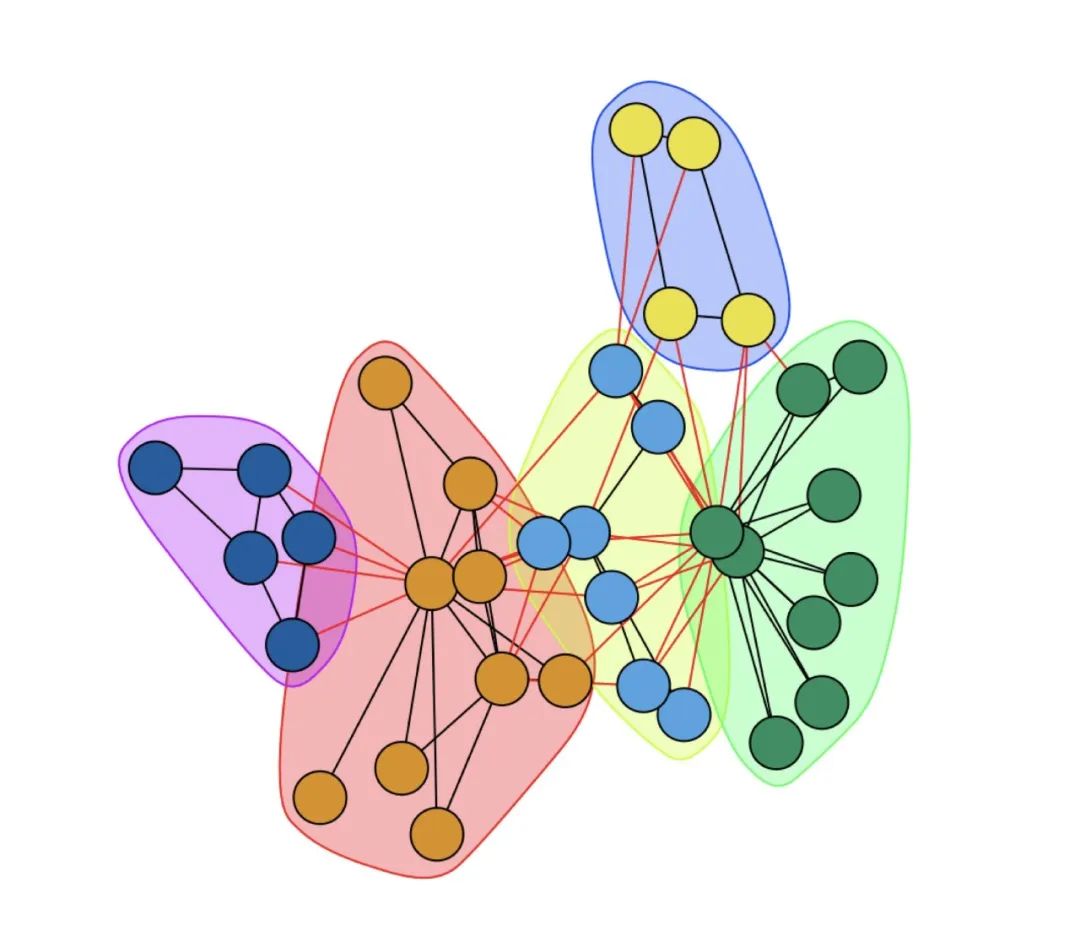
library(igraph)library(d3Network)igraphDat <- read.graph(file = "/Users/wuzhengxiang/Documents/PPT模板/0.edges", directed = FALSE)
## Simplify to remove duplications and from-self-to-self loopsigraphDat <- simplify(igraphDat, remove.multiple = TRUE, remove.loops = TRUE )
## Give numbersV(igraphDat)$label <- seq_along(V(igraphDat))
## Average path length between any two given nodes(averagePathLength <- average.path.length(igraphDat))
## Community structure detection based on edge betweennesscommunityEdgeBetwn <- edge.betweenness.community(igraphDat)
## Check the transitivity of a graph (probability that the adjacent vertices of a vertex are connected)(transitivityDat <- transitivity(igraphDat, type = "localaverage", isolates = "zero") )
## Set the seed to get the same resultset.seed("20200513")
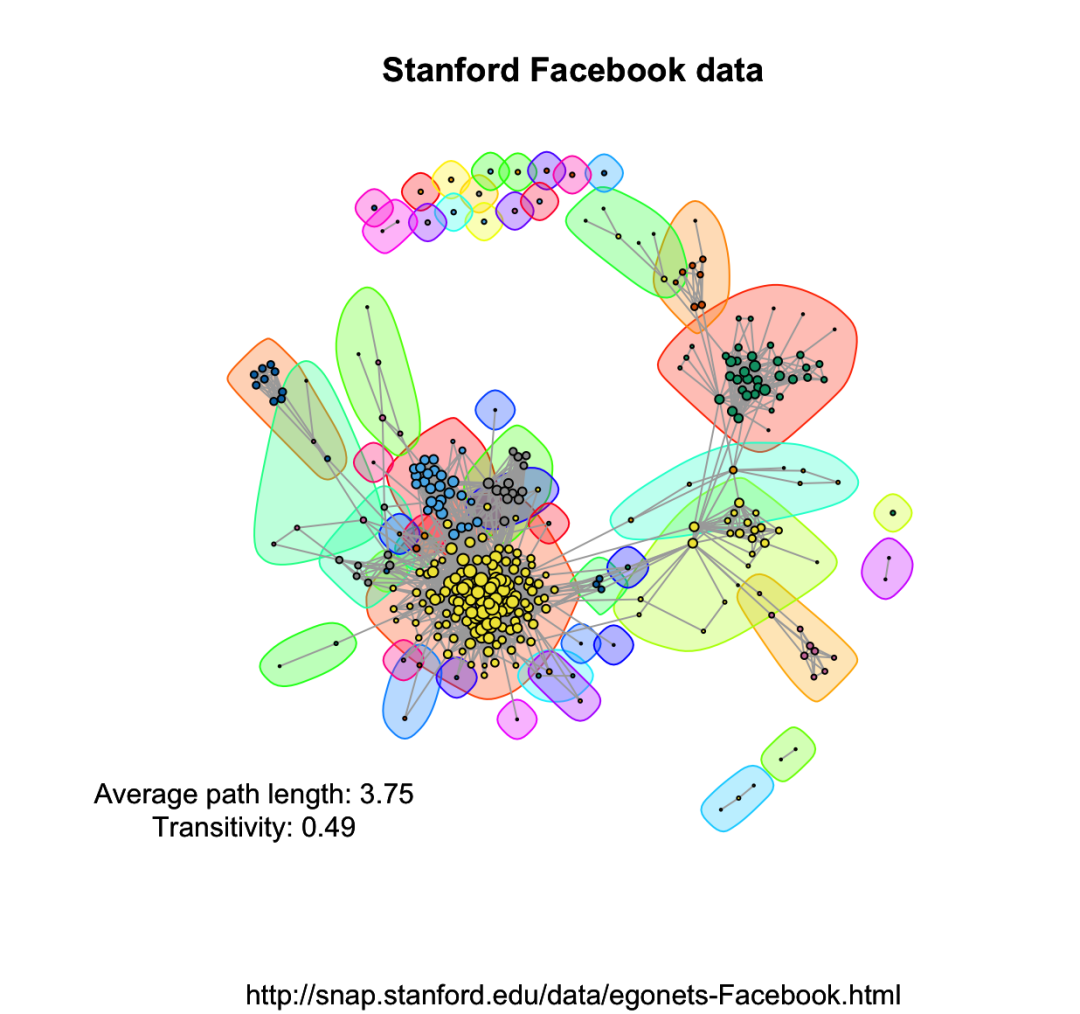
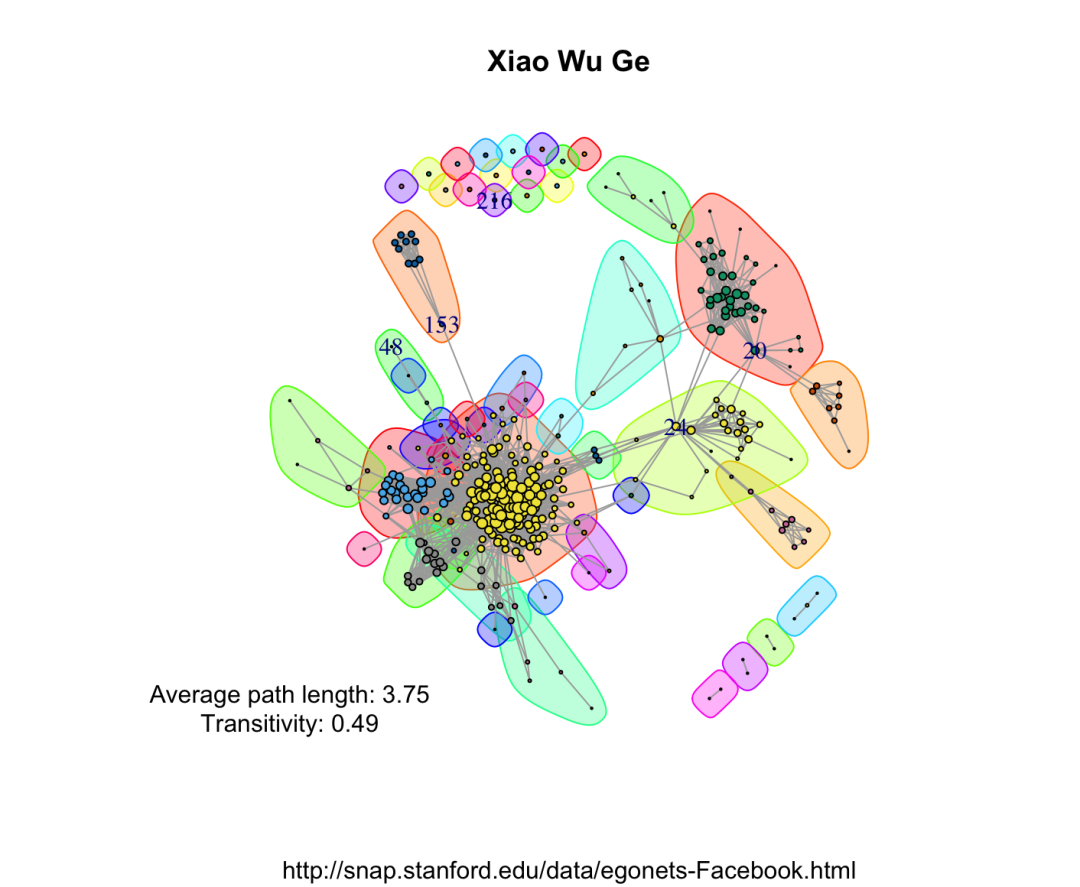
## Add community indicating background colorsplot(igraphDat,vertex.color = communityEdgeBetwn$membership, vertex.size = log(degree(igraphDat) + 1),mark.groups = by(seq_along(communityEdgeBetwn$membership), communityEdgeBetwn$membership, invisible) )
## Annotatetitle("Stanford Facebook data", sub = "http://snap.stanford.edu/data/egonets-Facebook.html" )text(x = -1, y = -1, labels = sprintf("Average path length: %.2fnTransitivity: %.2f", averagePathLength, transitivityDat) )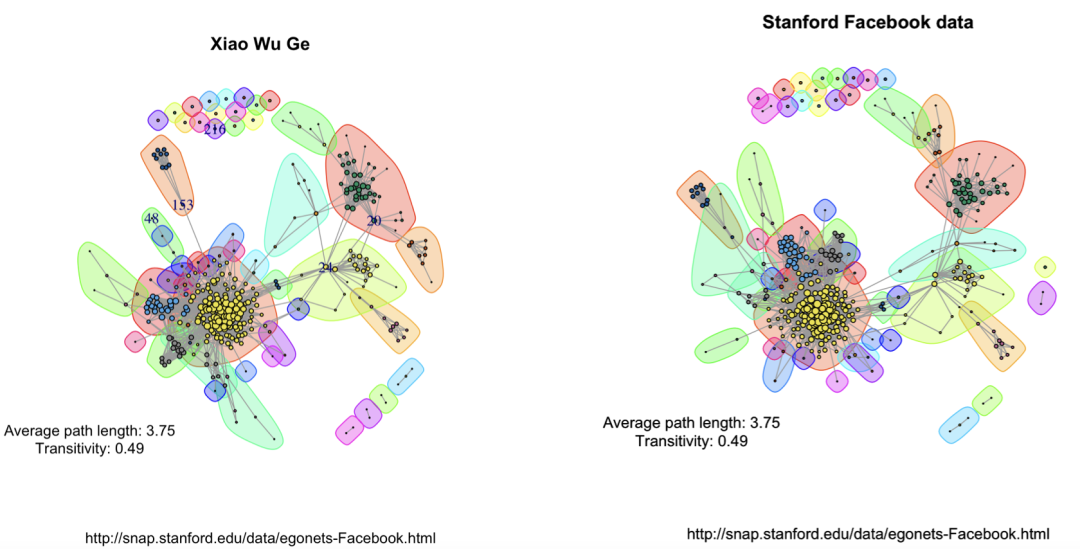
四、算法优缺点
1、算法优点
无须定义优化函数,无须事先指定社区个数,算法会利用自身的网络结构来指导标签传播。
2、算法缺点