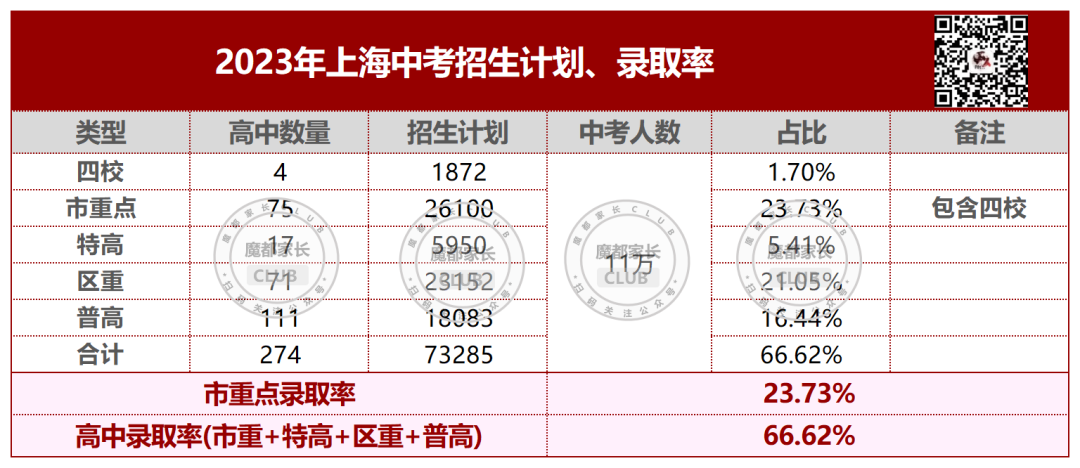
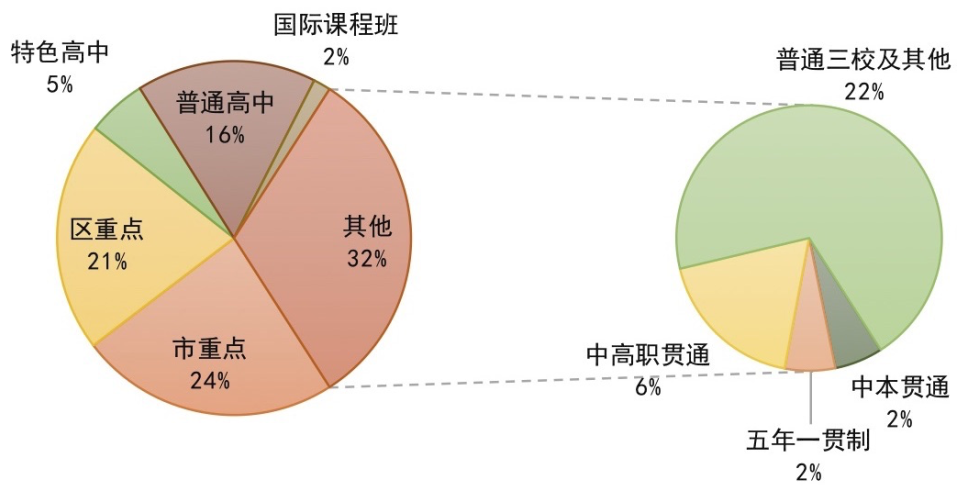
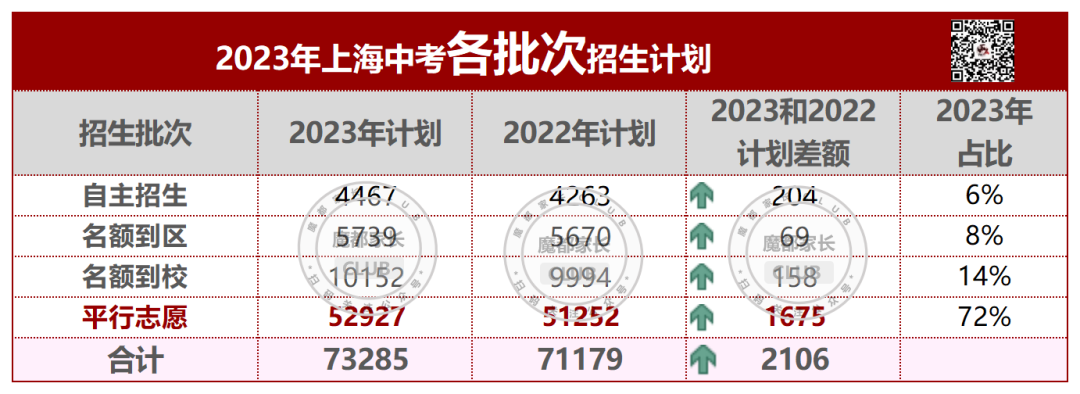
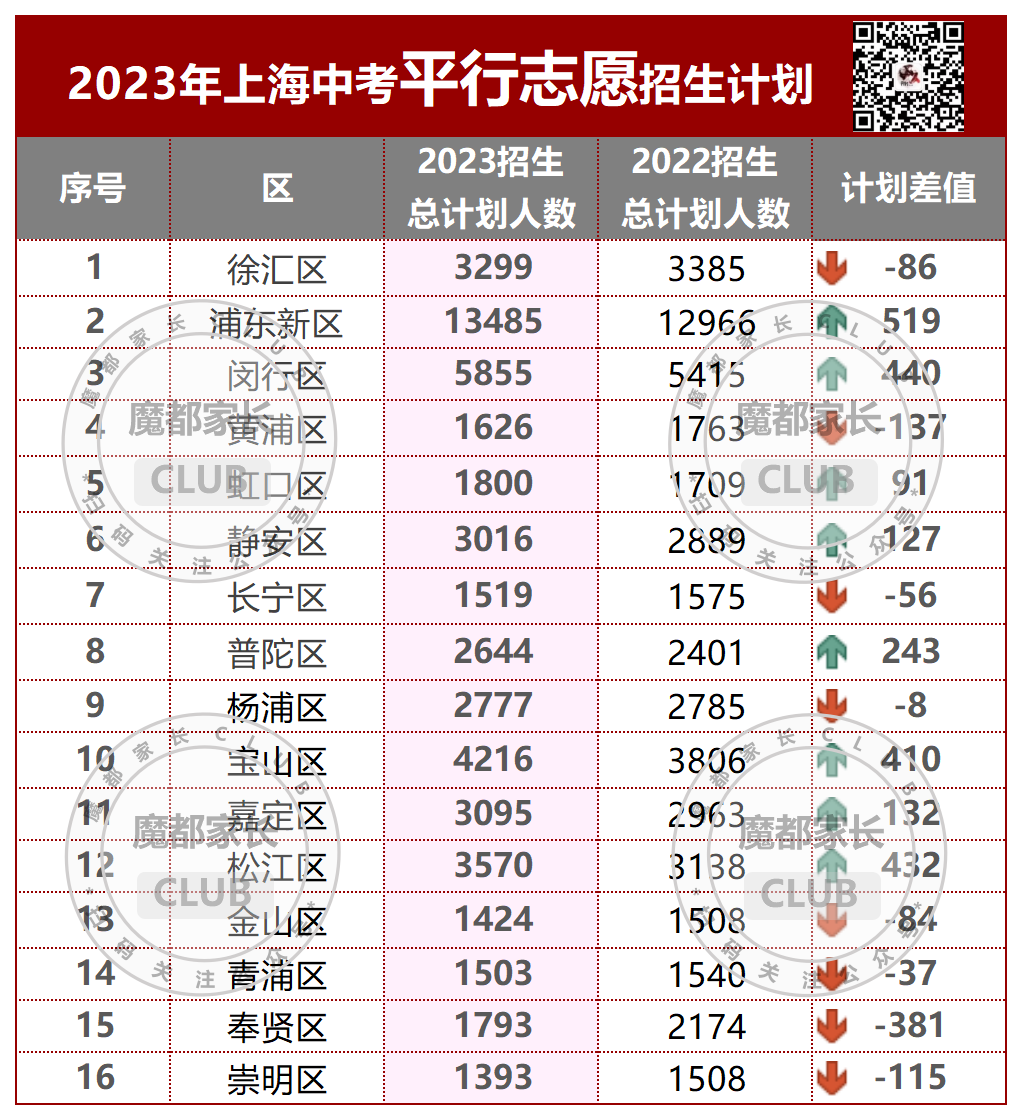
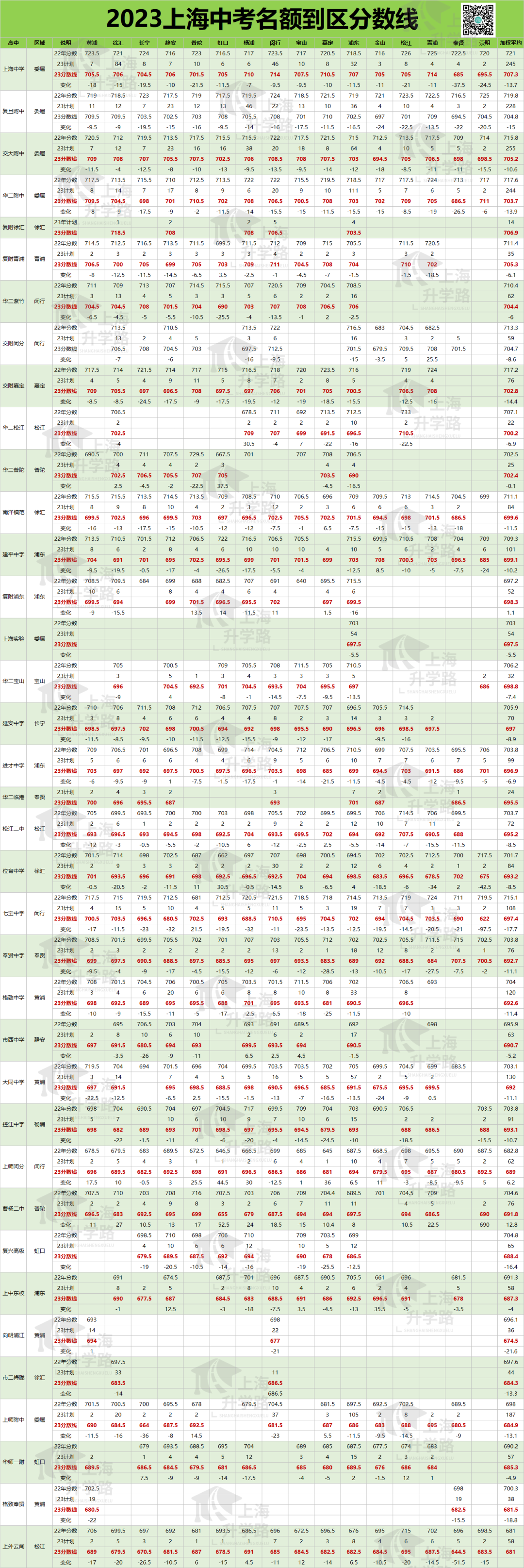
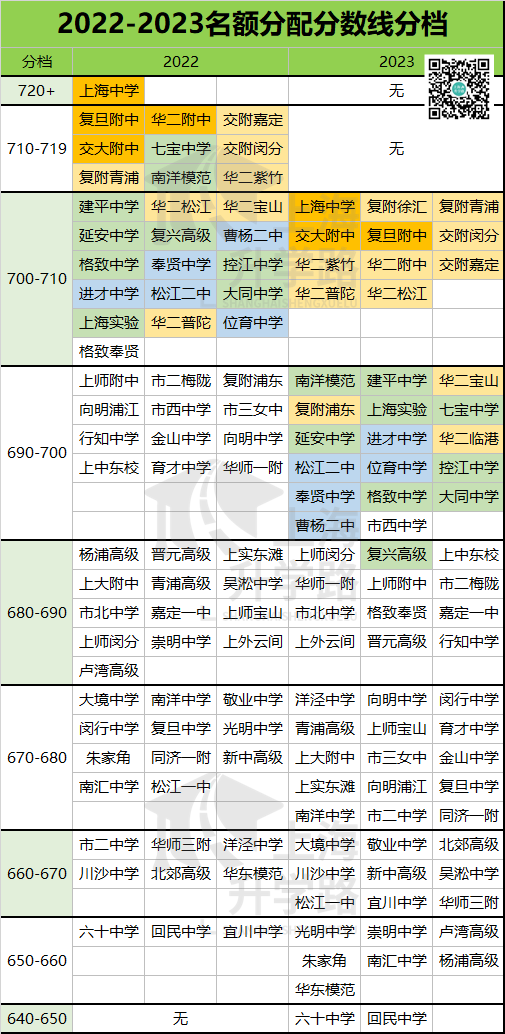
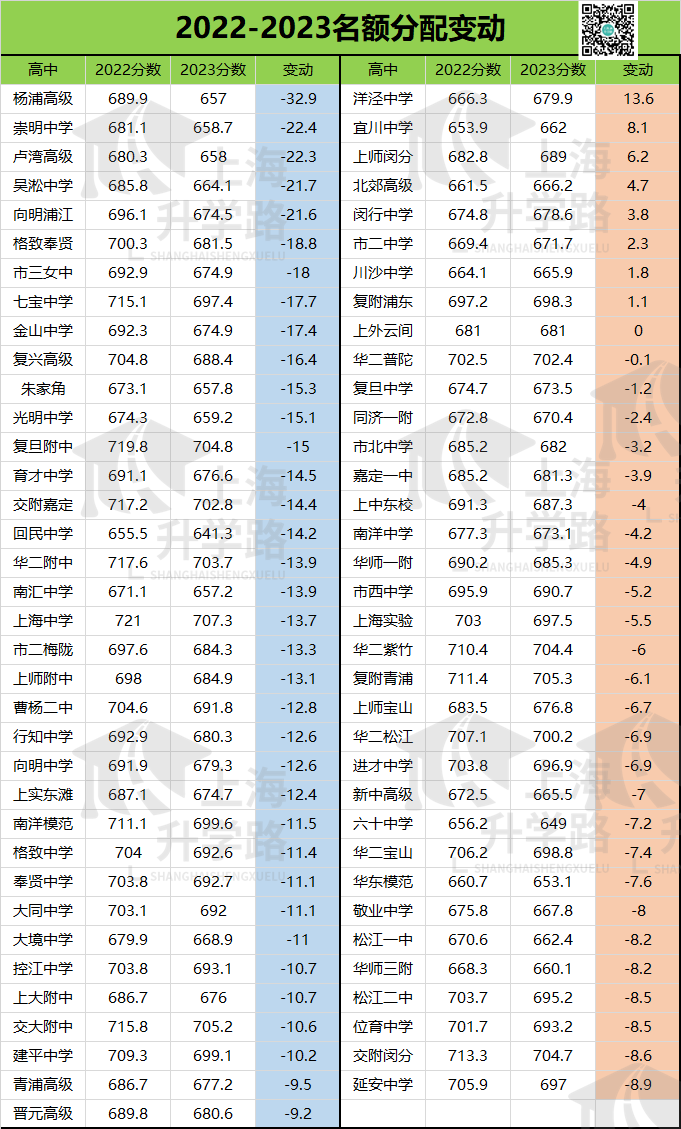
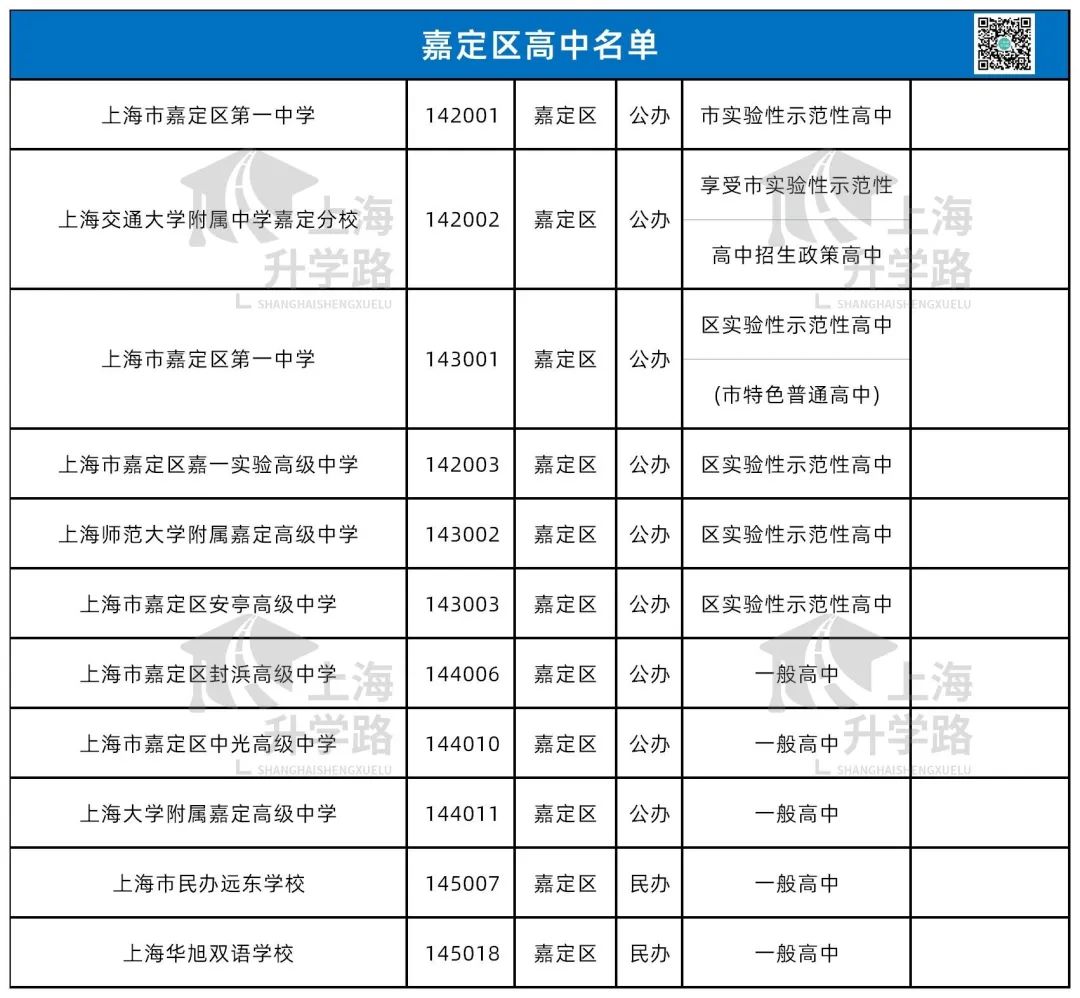
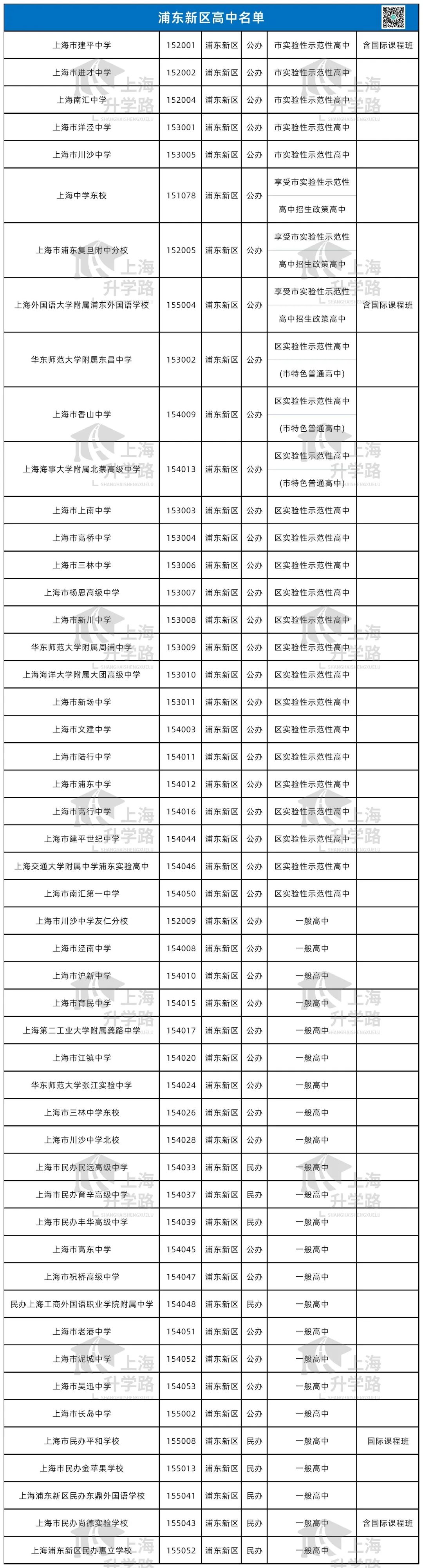
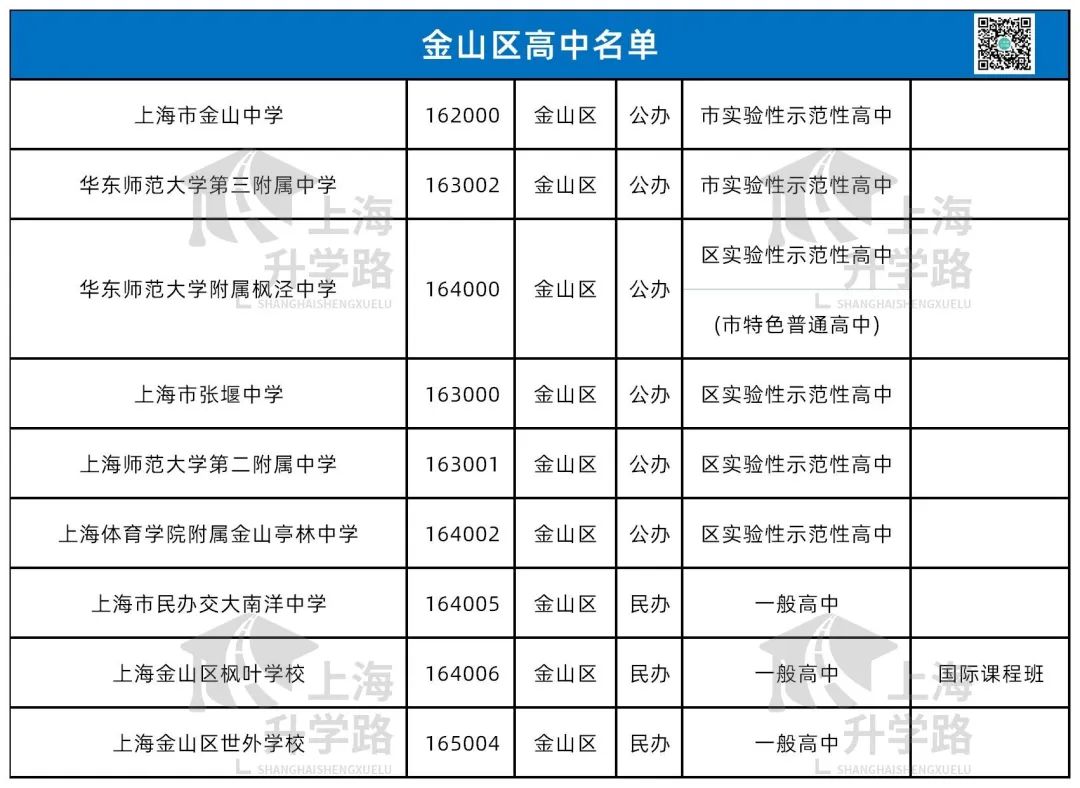
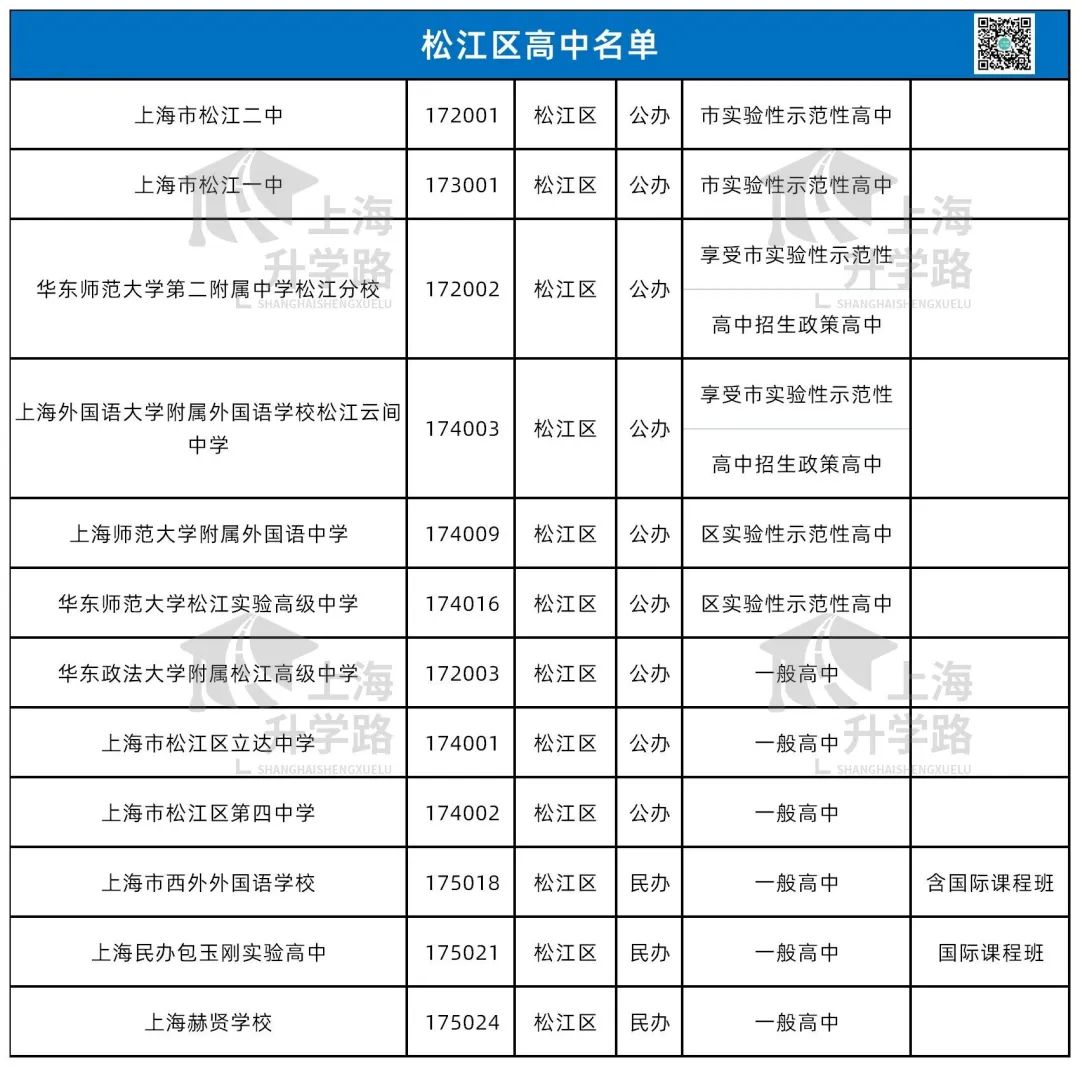
2023年中考已经落幕,从偷摸自招到中考难哭,从家长焦虑不安到分数狂降10分,这届中考家长和同学们可以说是承受太多。
回望这届中考,各个区都表现如何?
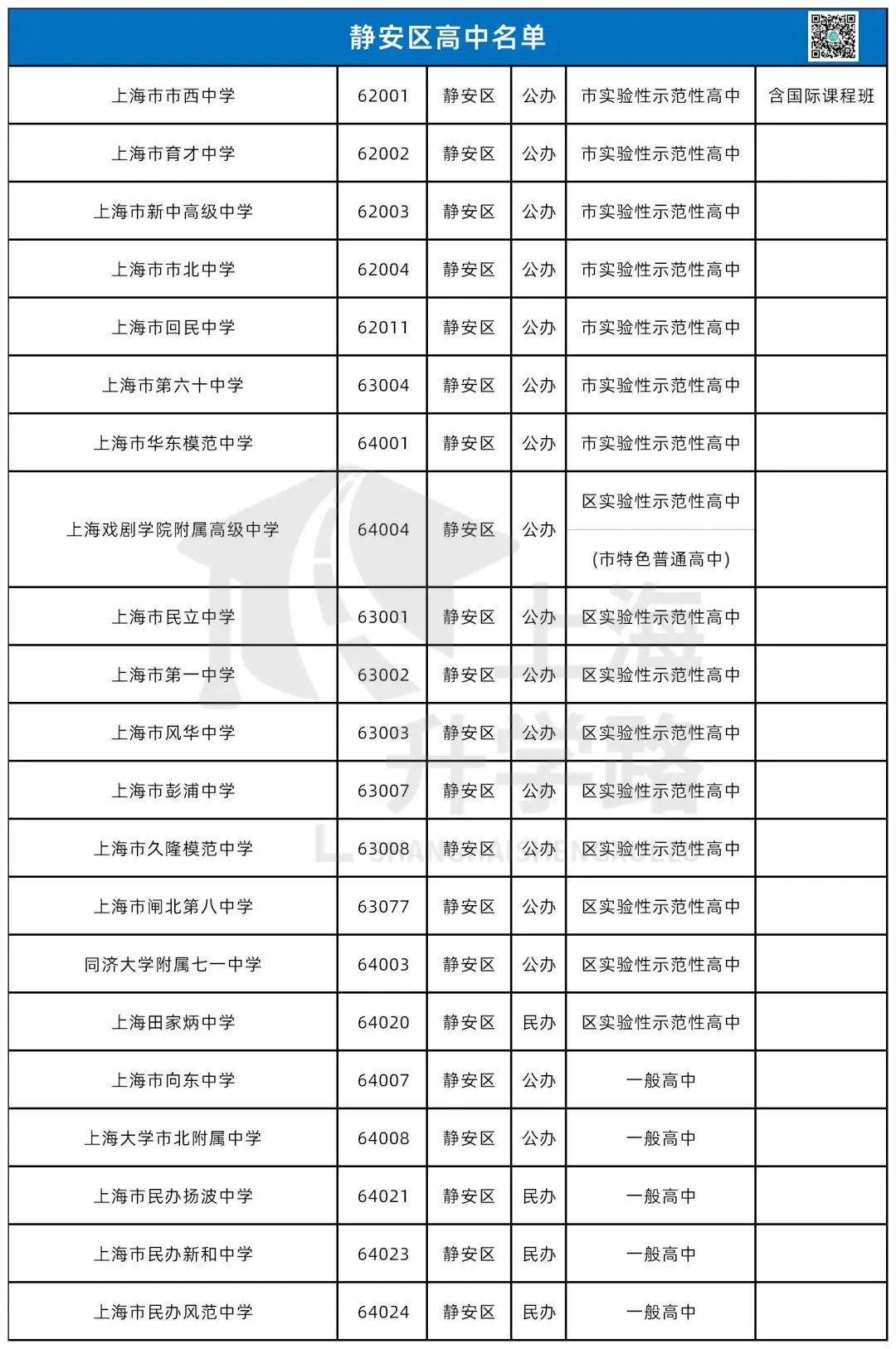
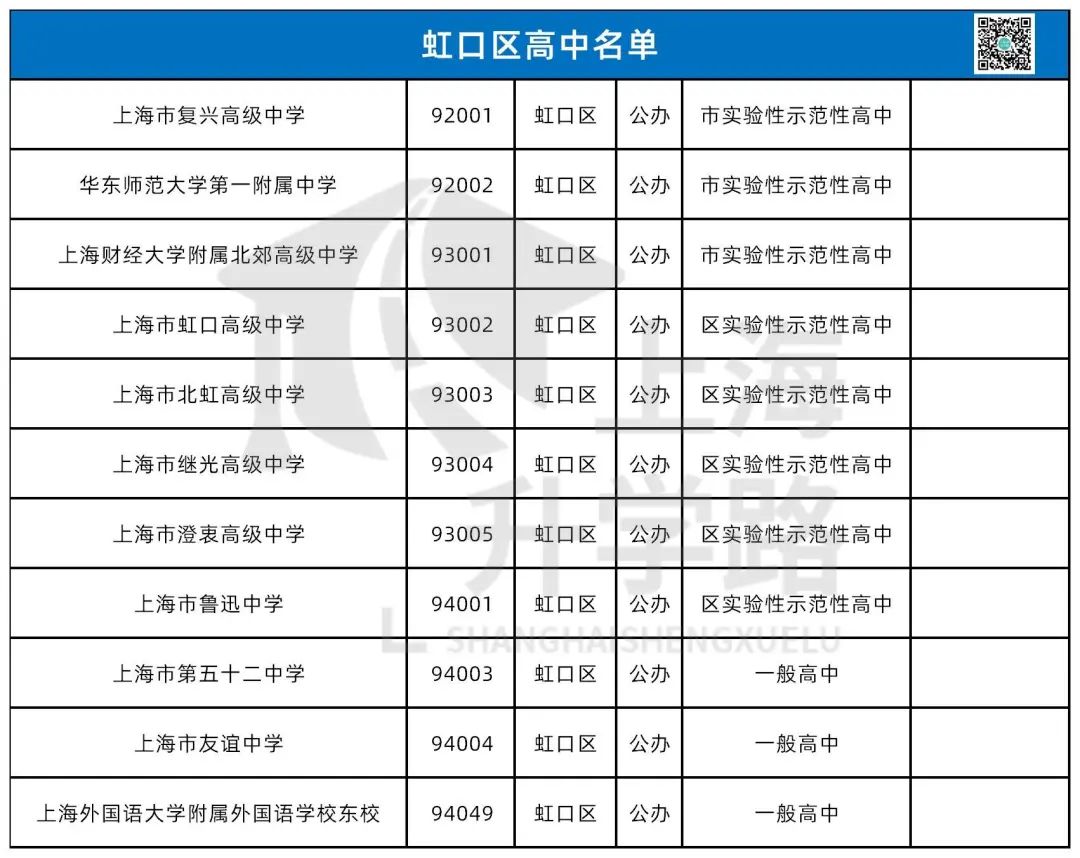
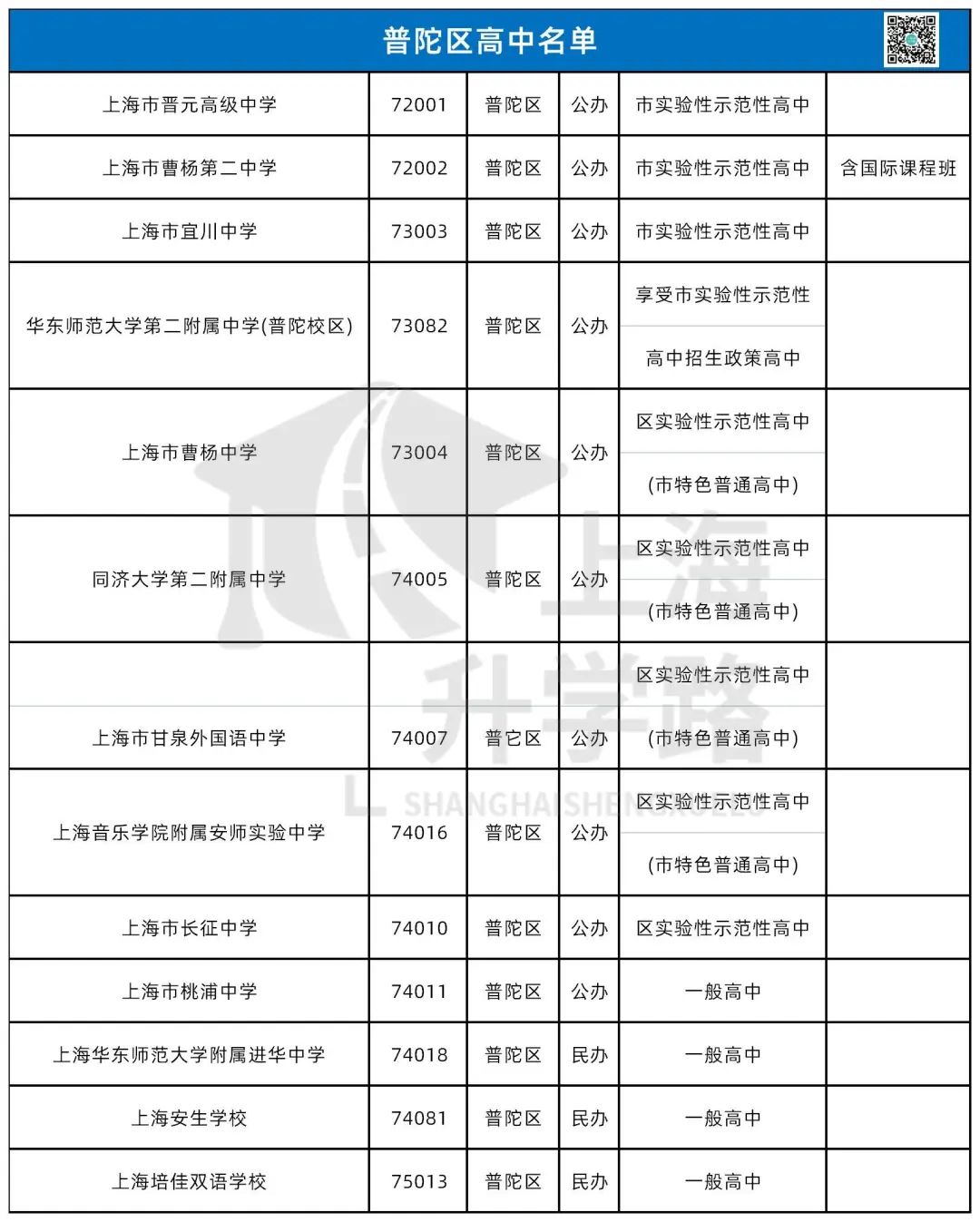
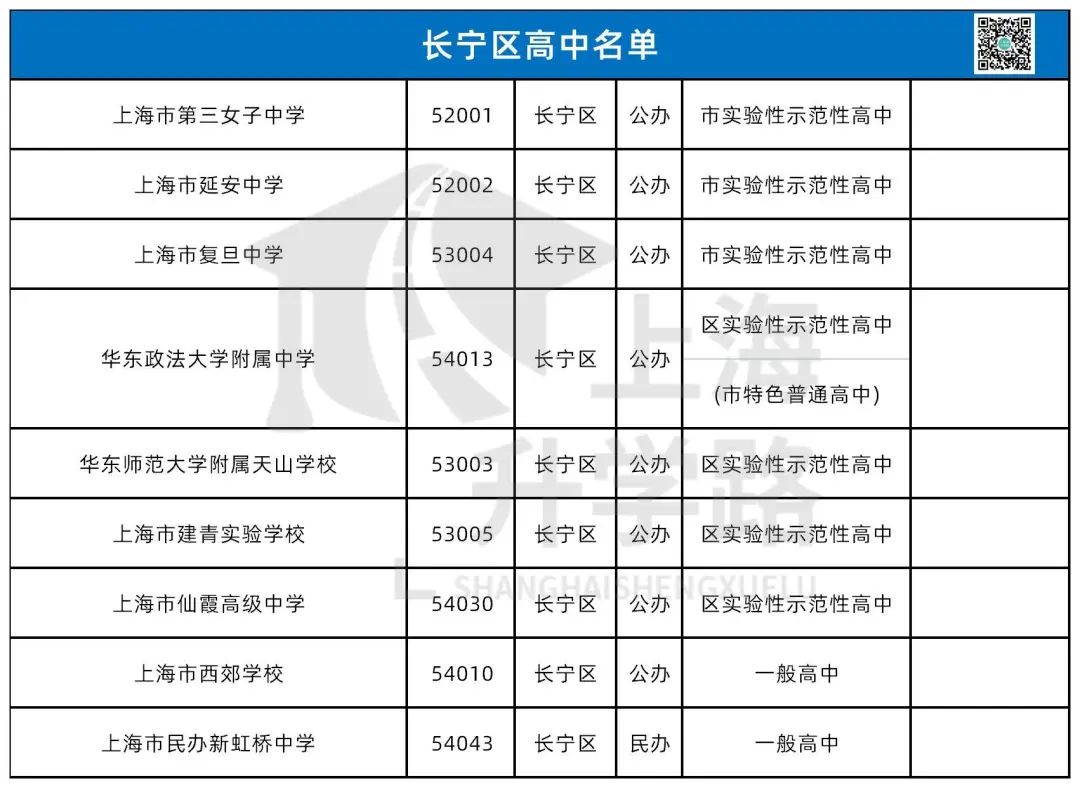
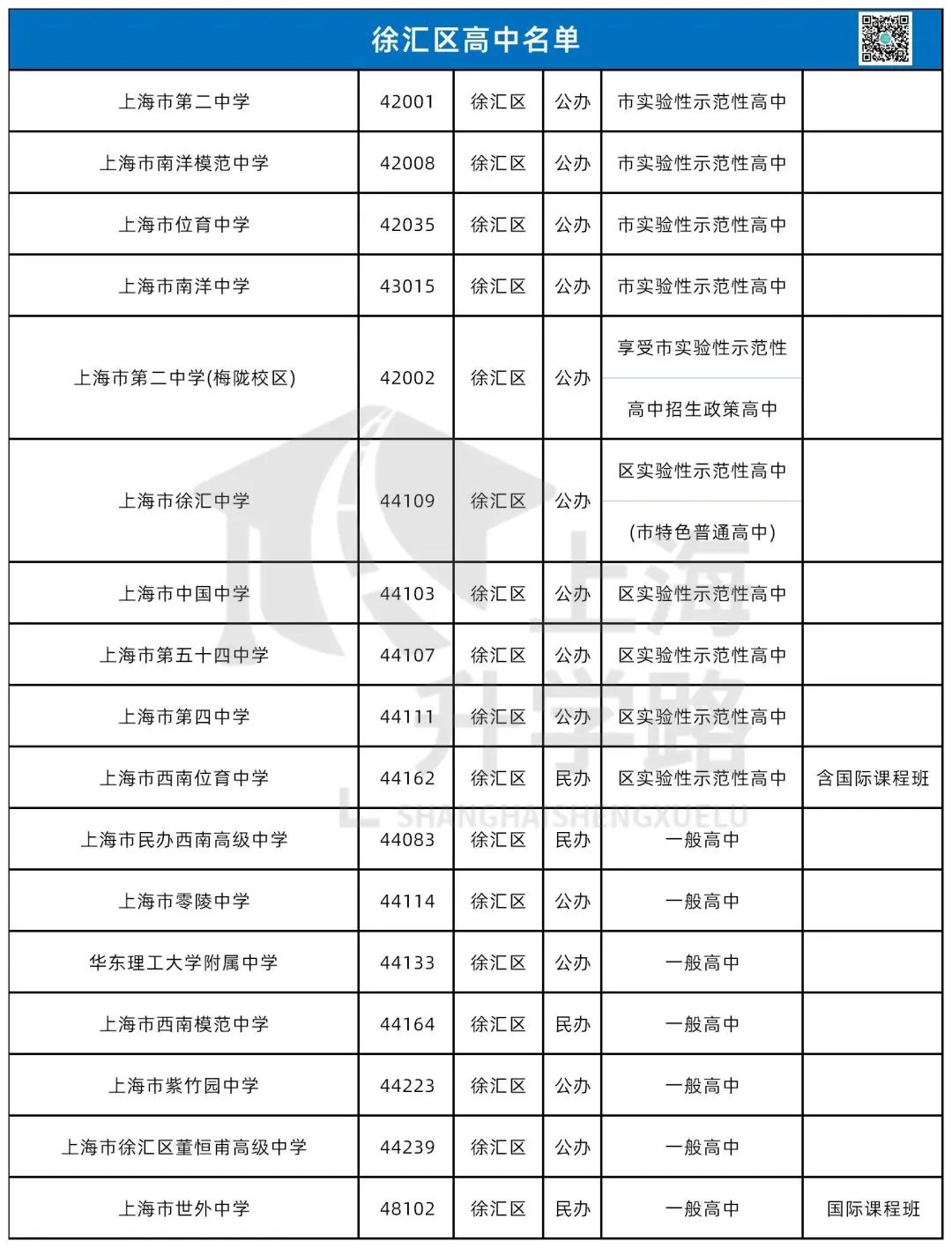
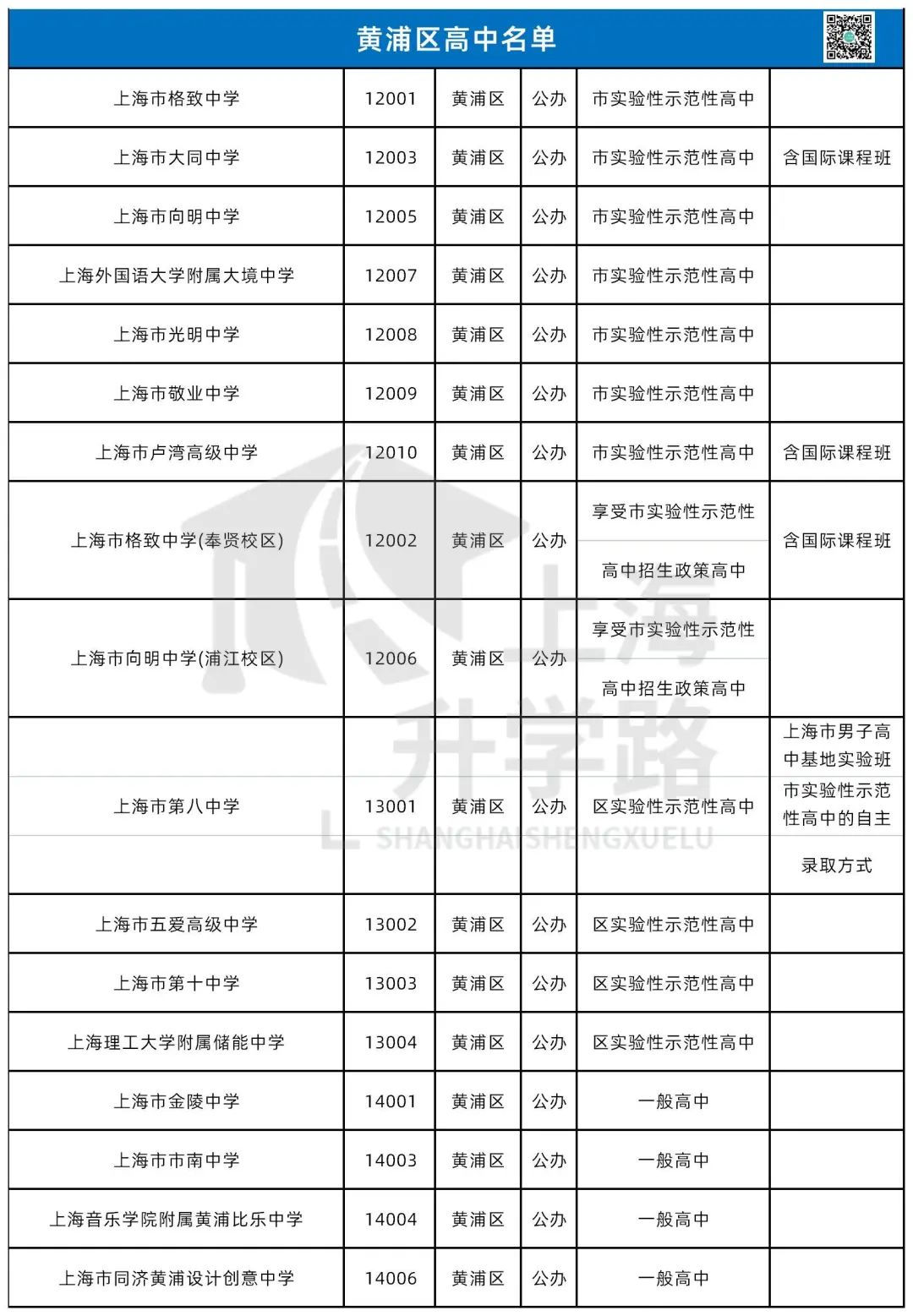
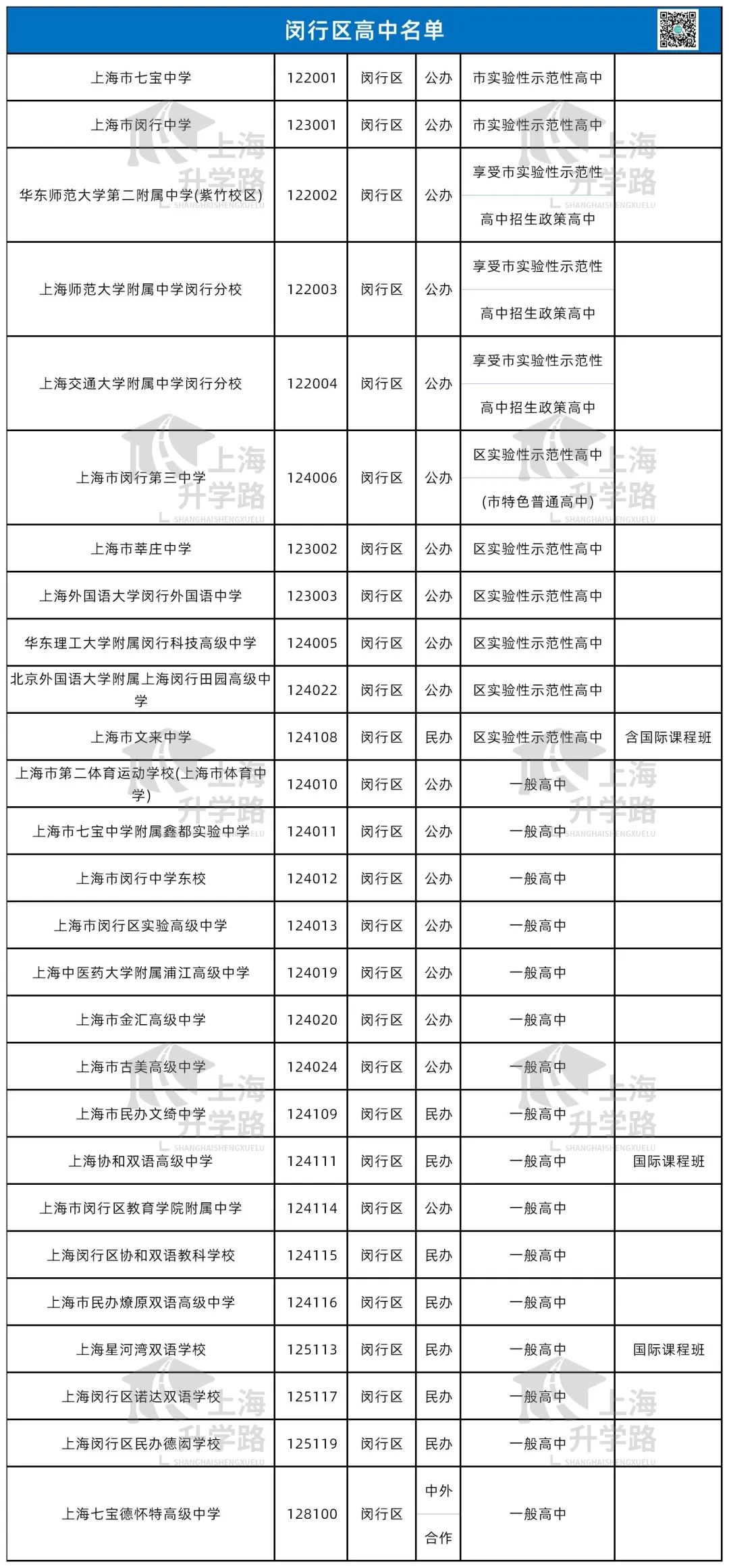
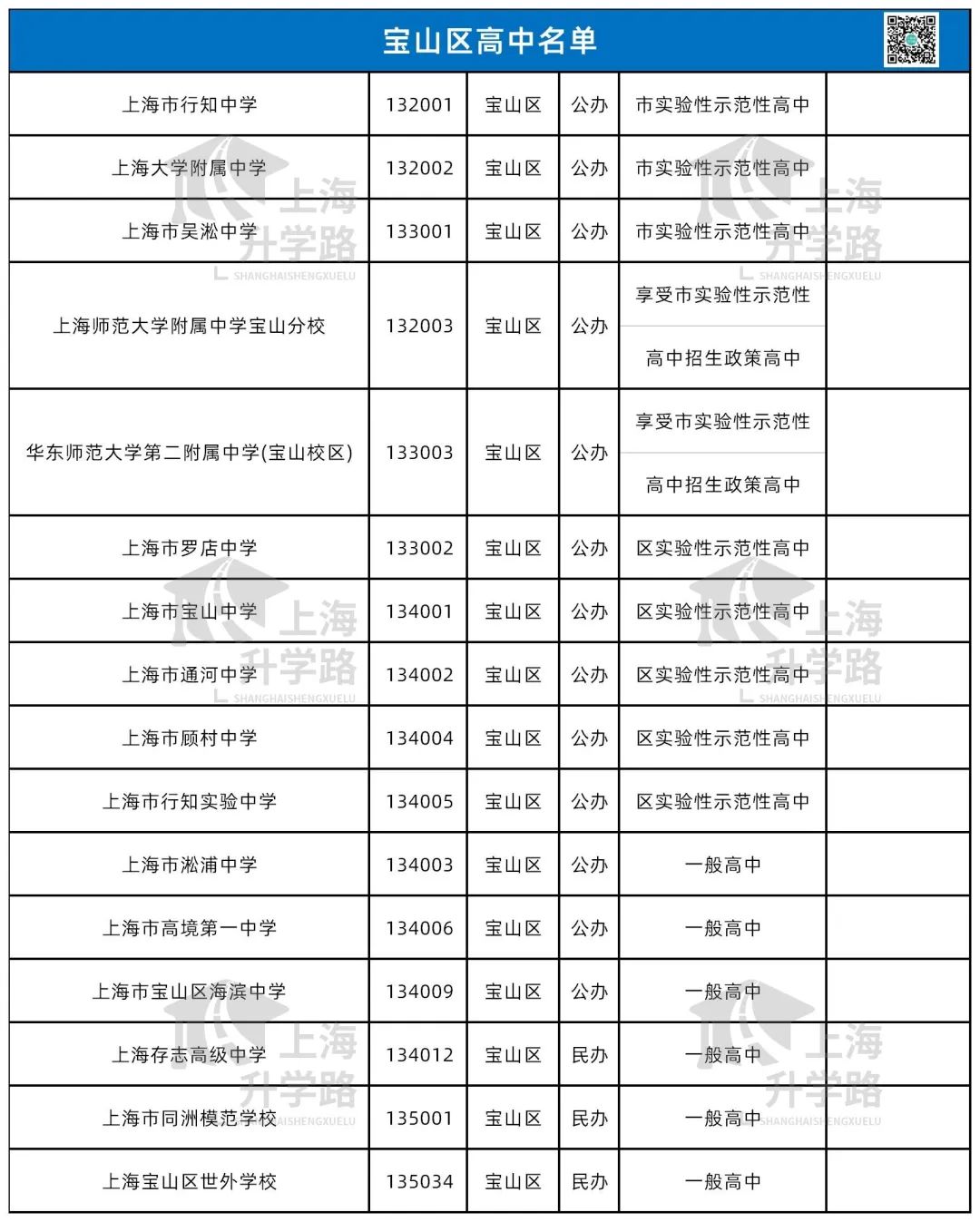
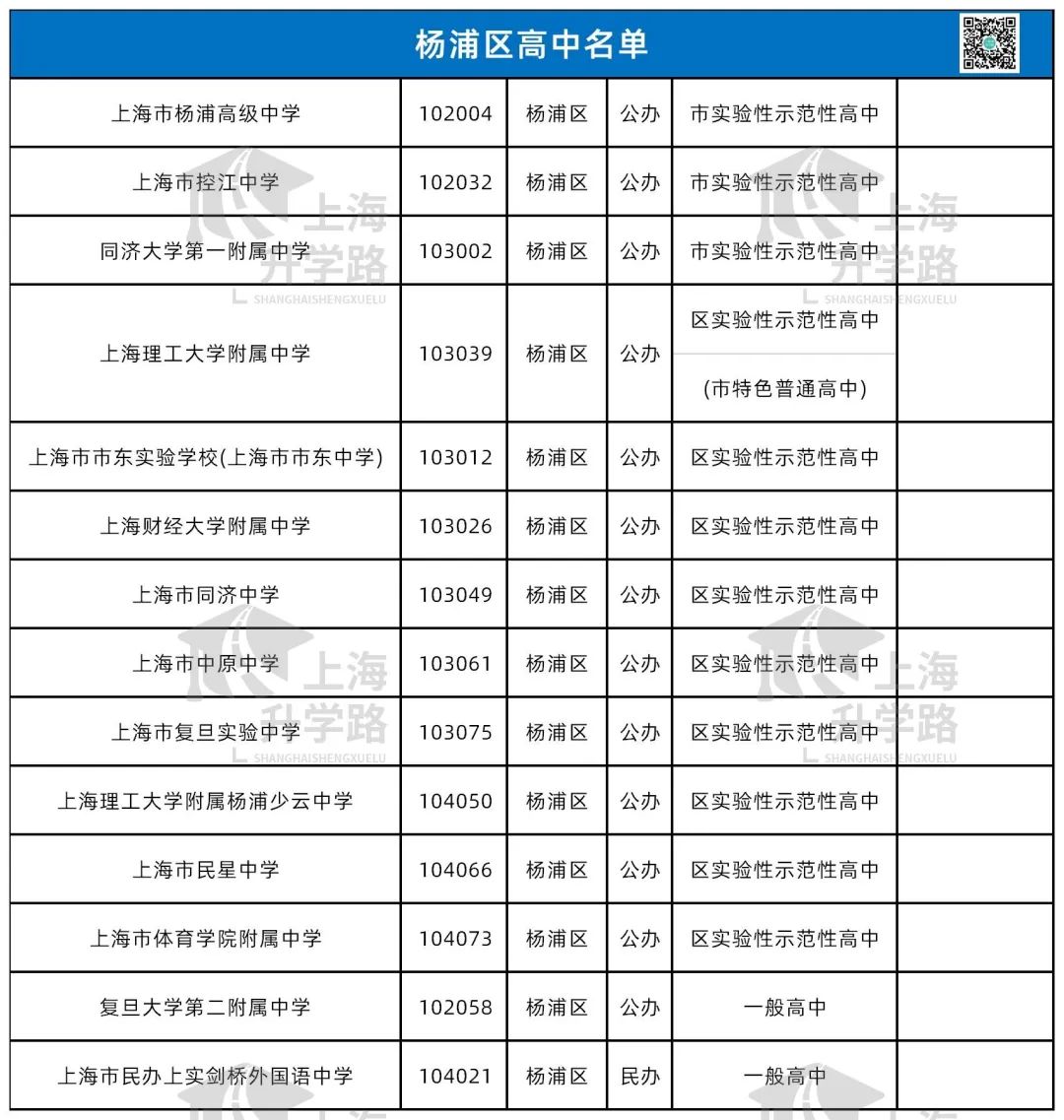
今天我们要回望的是——杨浦区,这个和徐汇并称为“南徐汇,北杨浦”的教育强区。

2023年中考人数:6236人
高中总计:14(+2)所
四大名校:复旦附中,交大附中,四校f4有两所
八大金刚:控江中学
其他市重:2所,杨浦高级,同济一附
特色普高:1所,上理附中
区重点:8所
普通高中:2所
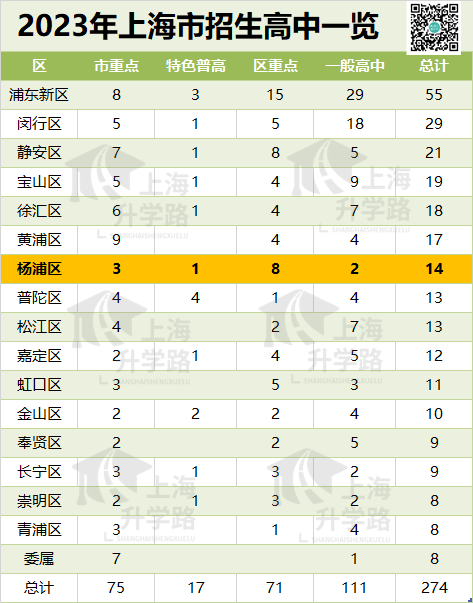

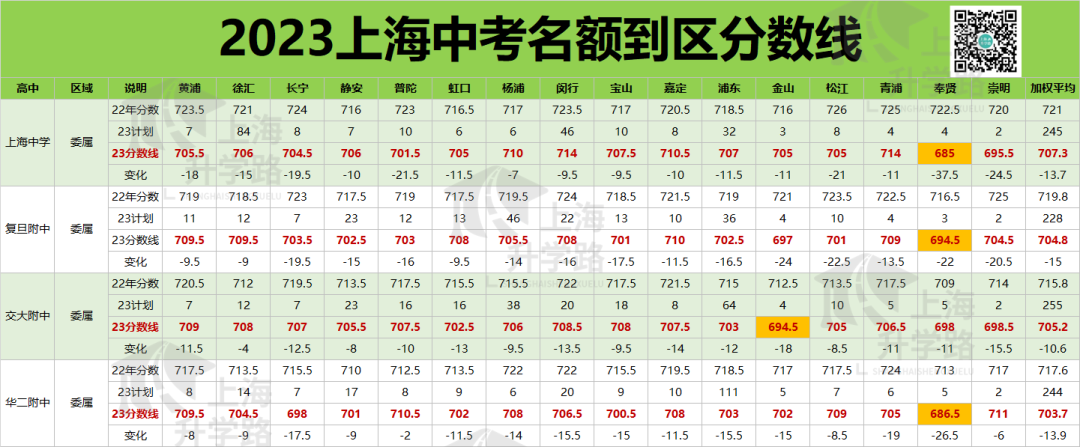
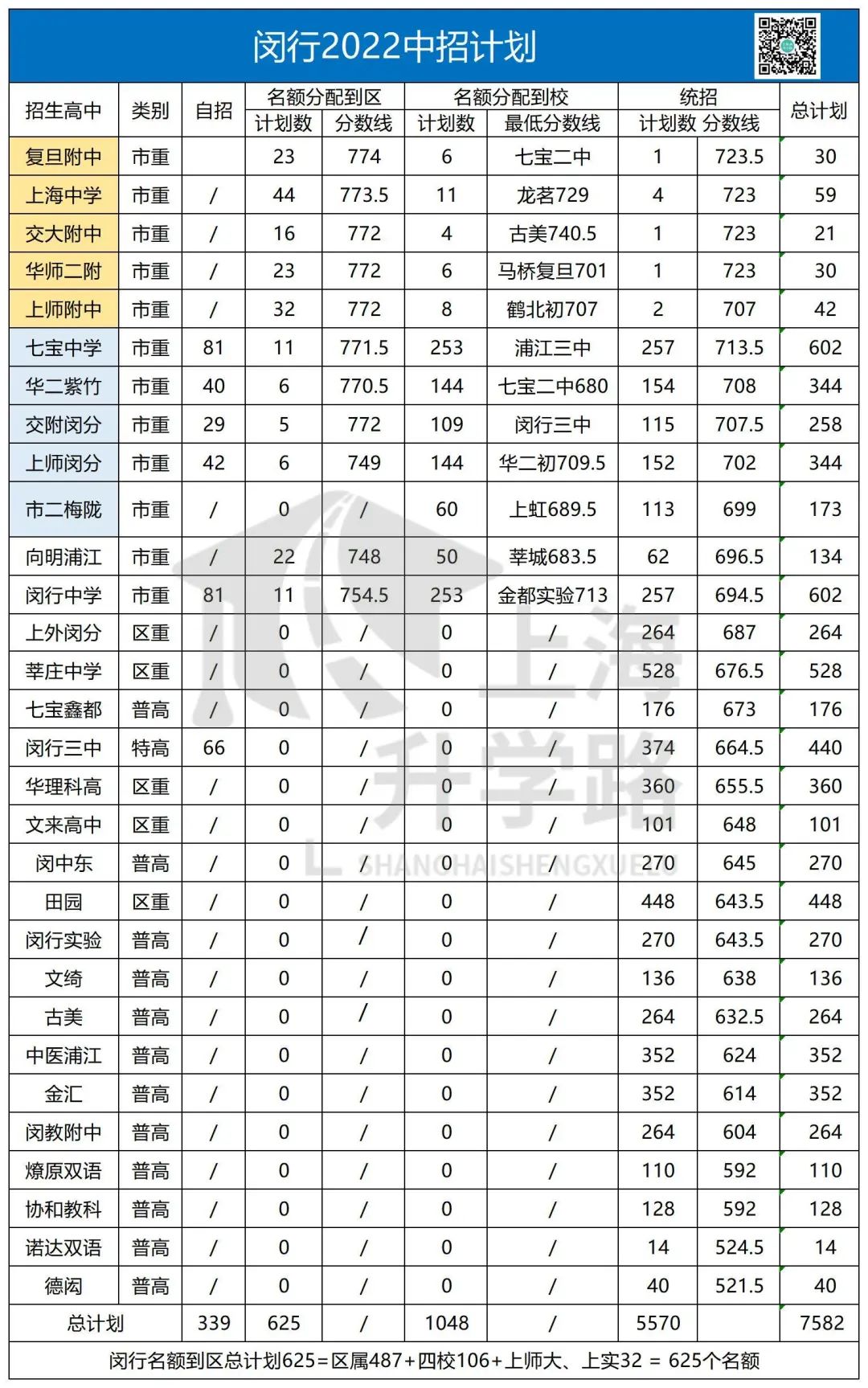
2023年杨浦区的招生计划如图所示。
如果把区内市重和特色普高的自招全算进去,2023年在杨浦区的招生计划共3993个,占总考生的64.03%。
其中,委属123个,占比1.97%(这里同样没算复附交附的自招,像复附的大部分自招都被兰生瓜分,所以总比例是高于2%的);
市重点累计1556个,累计24.95%,这意味着杨浦有1/4的同学能去市重点;
区重点2164个,累计前59.65%的同学能进区重。杨浦区的一大特点就是区重比普高多。
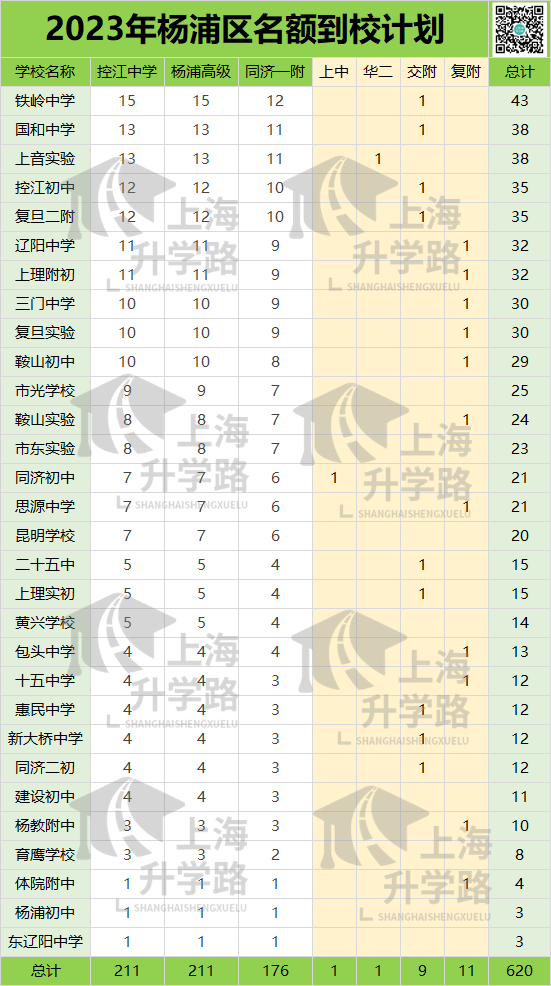
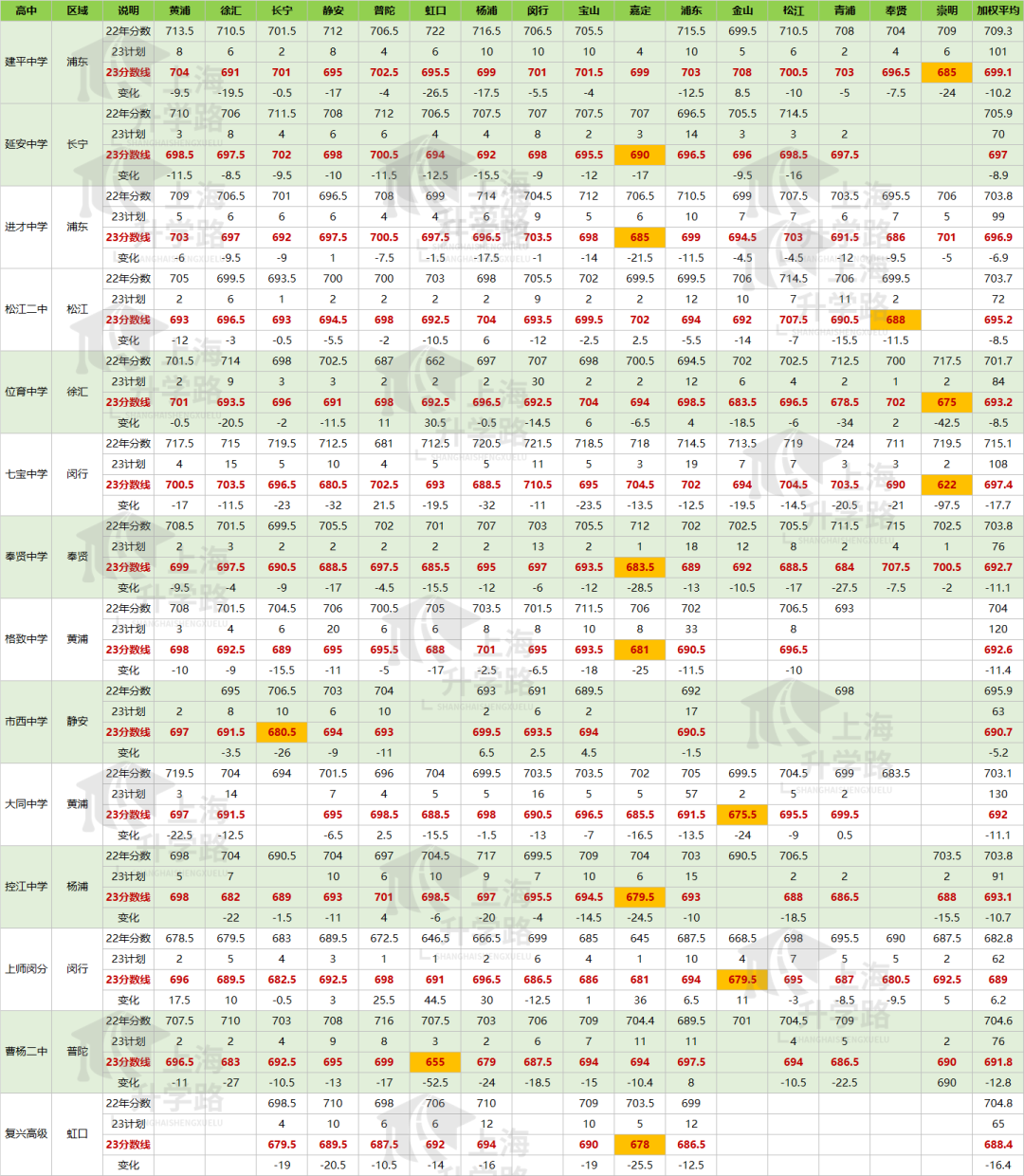
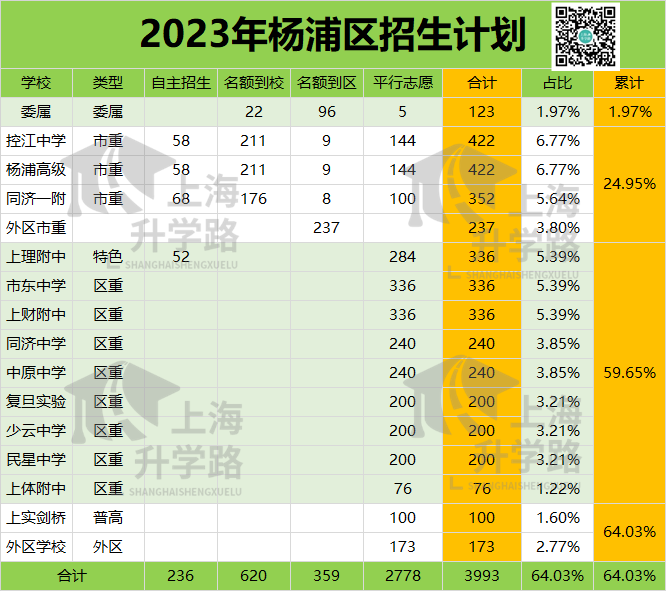
今年名额分配到校的计划如图所示。
杨浦区名额分配到校的计划共620个,受分初中学校共30所。
最多的是铁岭中学,有43个市重点的到校名额,意味着在没有自招、到区的情况下,需要在校内排名前43,才能进市重点。
最少的是杨浦初中和东辽阳中学,仅有3个。
根据测算,2024年公办被分到的名额到校名额有可能会缩水16.5%。

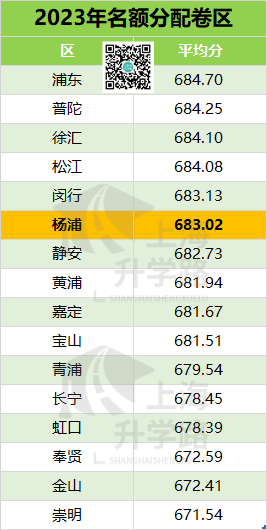
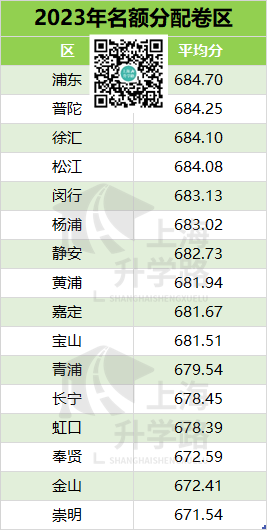
从名额分配的平均分来看,徐汇区的分数高达683.02,在16个区里排在靠前的位置,但和第一差距不到2分,也算卷区了。
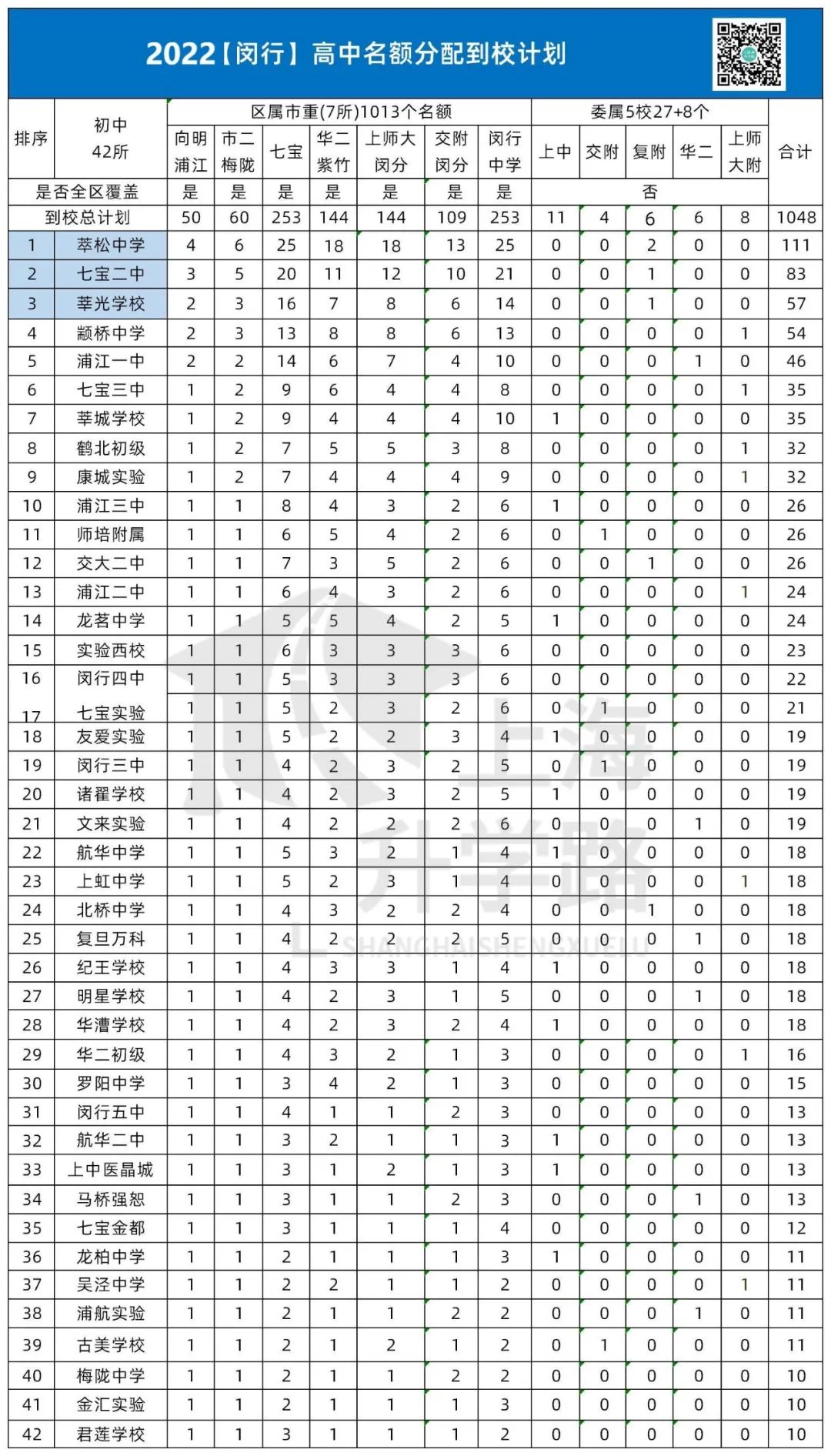
2023年名额分配到校如图所示。图比较大,可以点击放大查看。
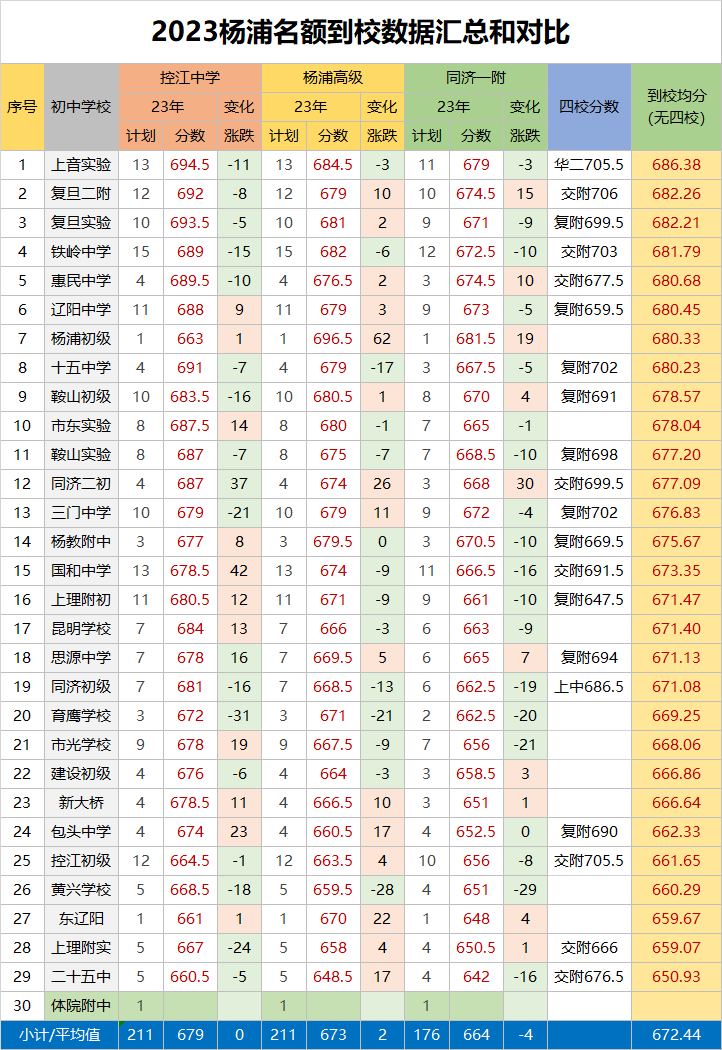
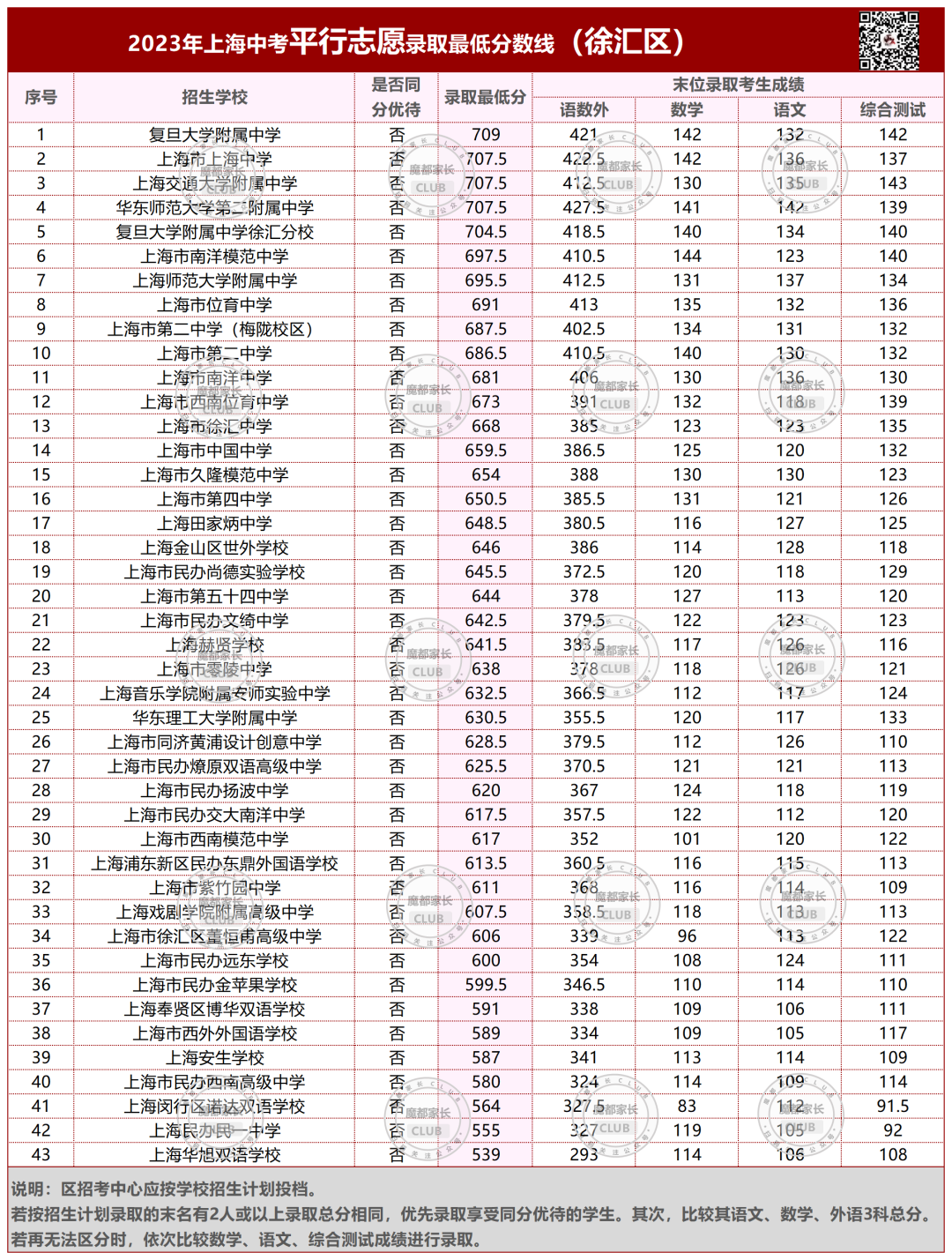
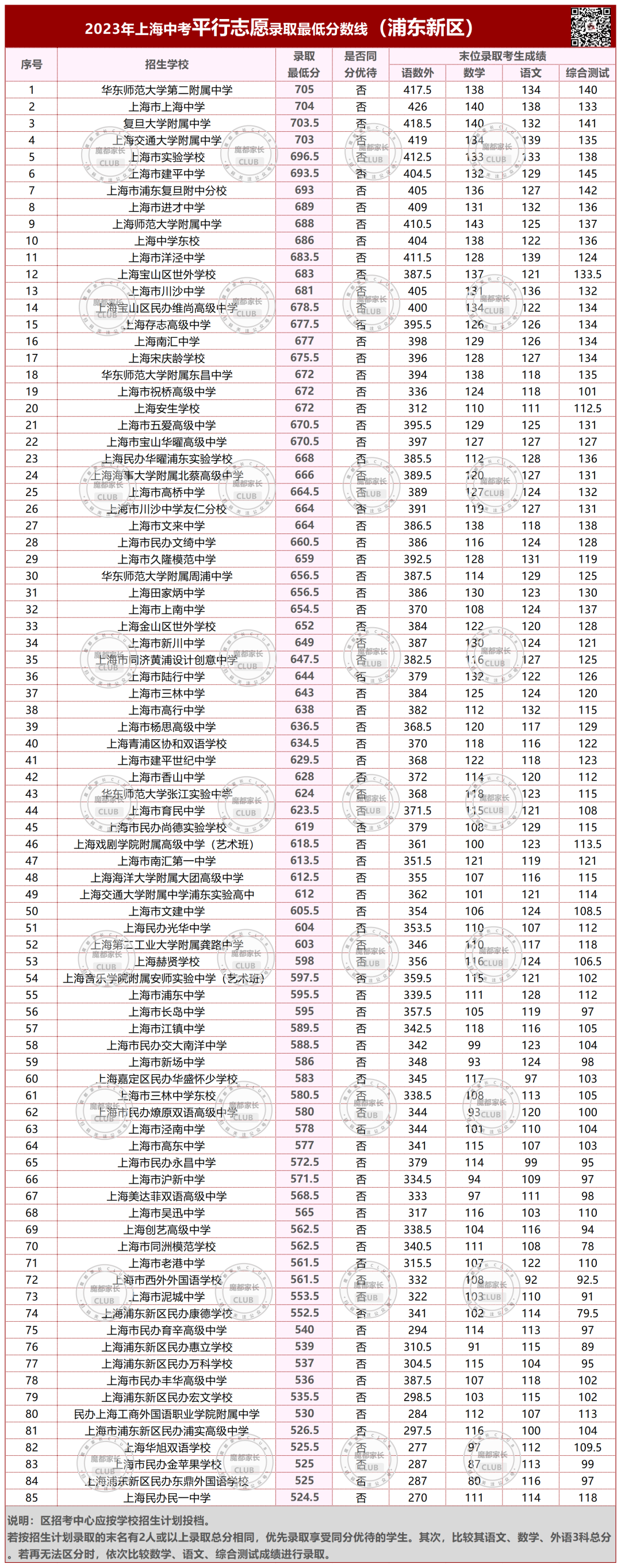
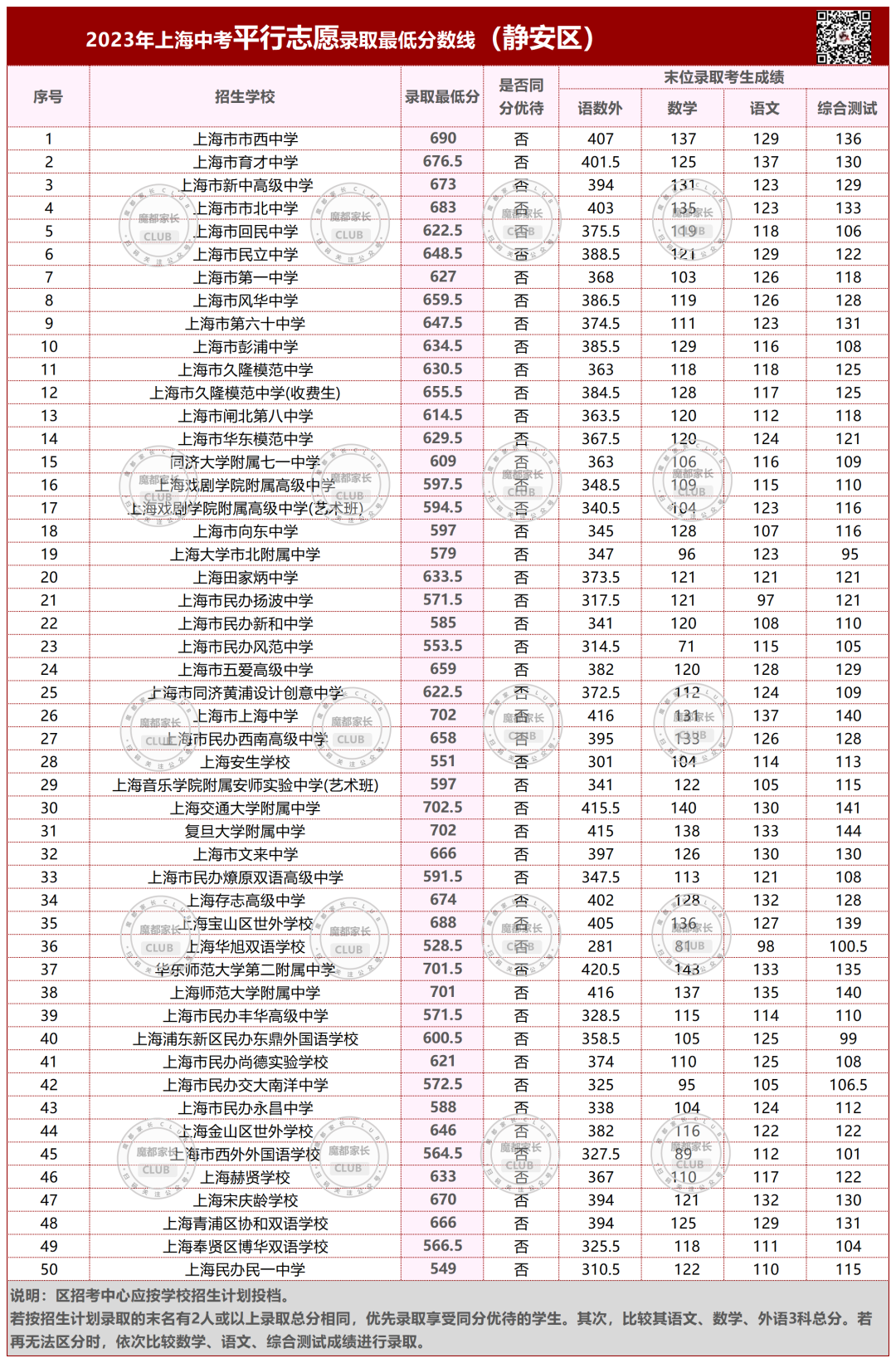
今年在徐汇区名额分配的3所学校里,最低分都在二十五中。
名额分配到校的均分排名,一定程度上可以表明这所公办培养尖子生的能力。
所以上音实验、复旦二附、复旦实验、铁岭中学、惠民中学算是杨浦区的top级别公办。
体院附中,四大皆空。这很难评价。
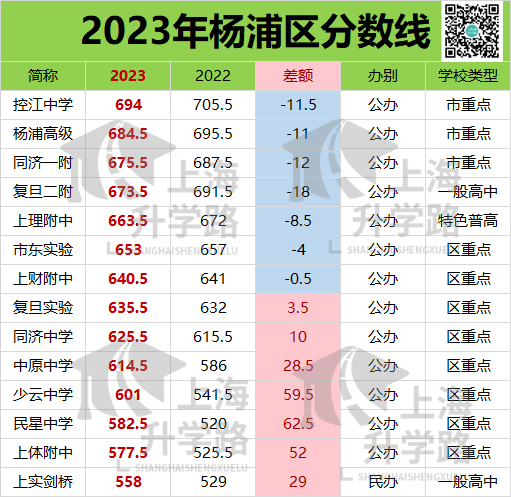
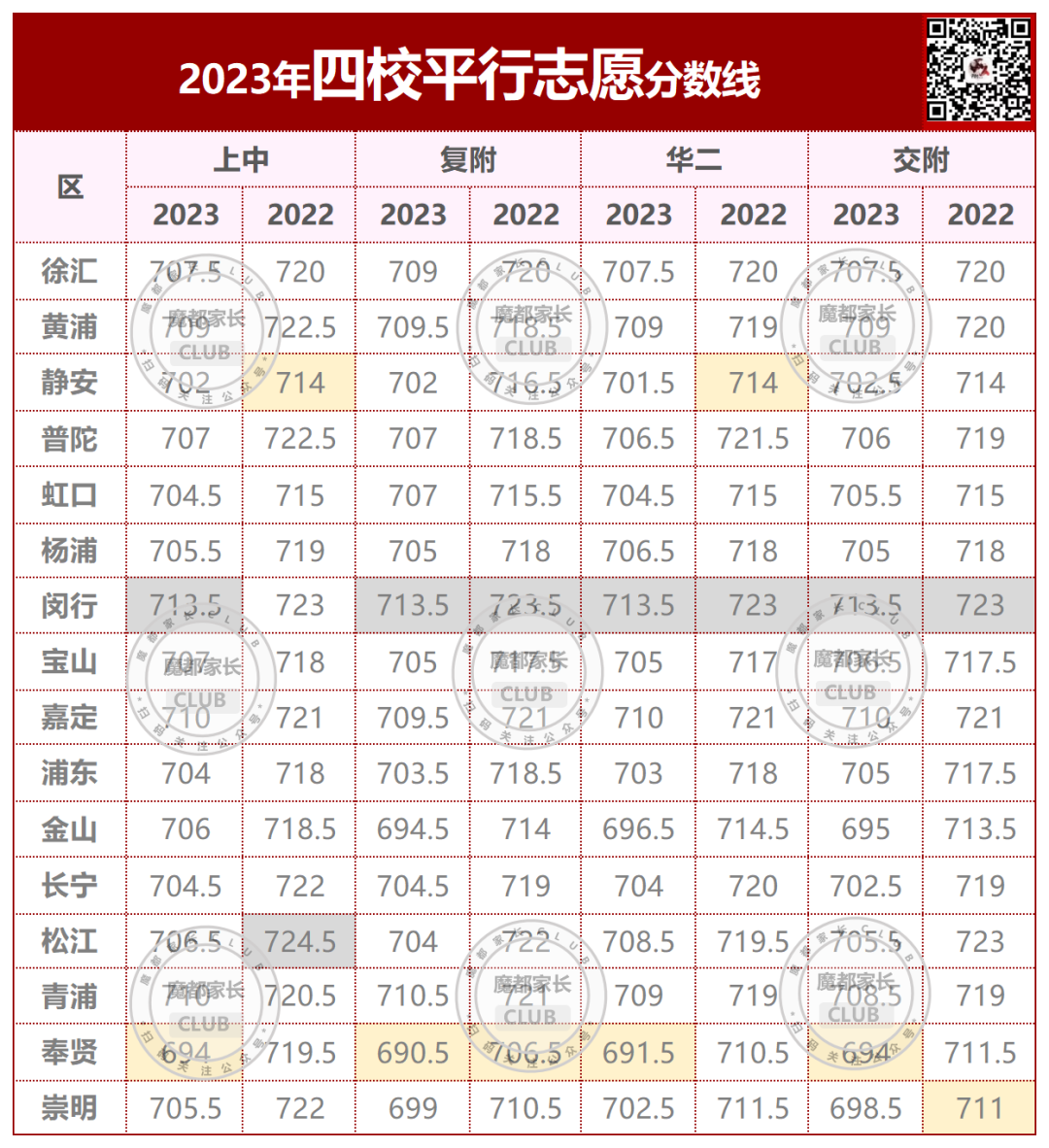
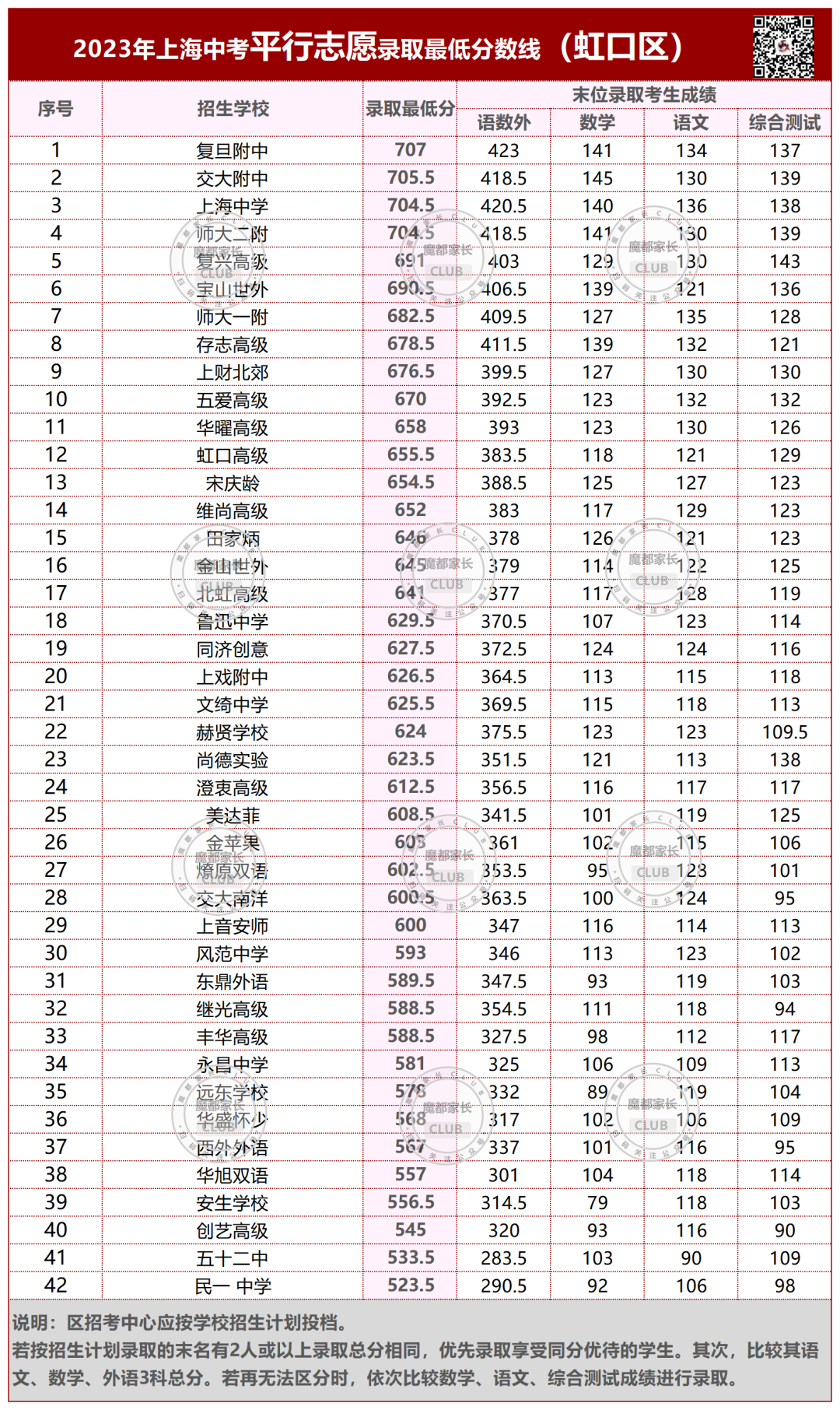
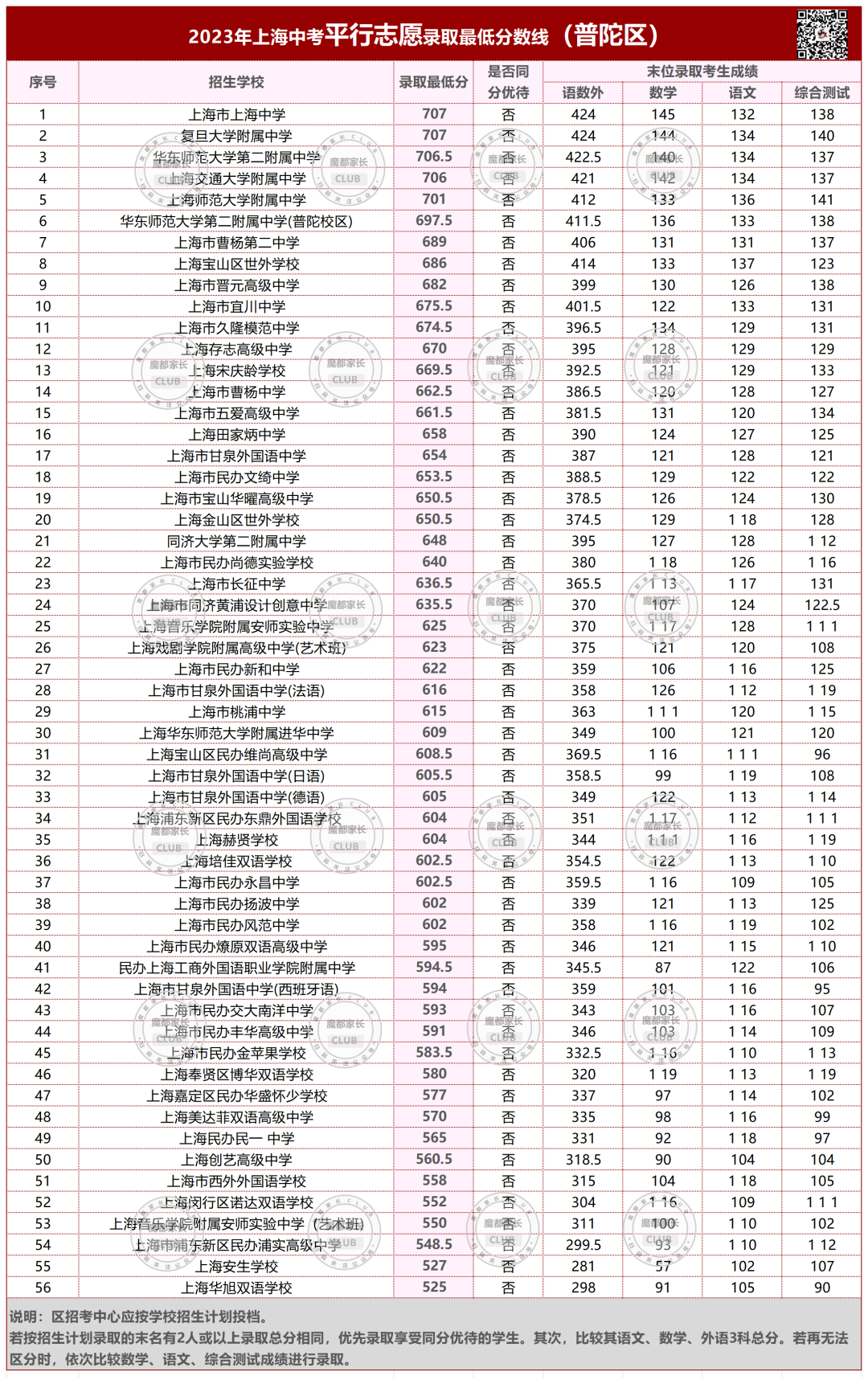
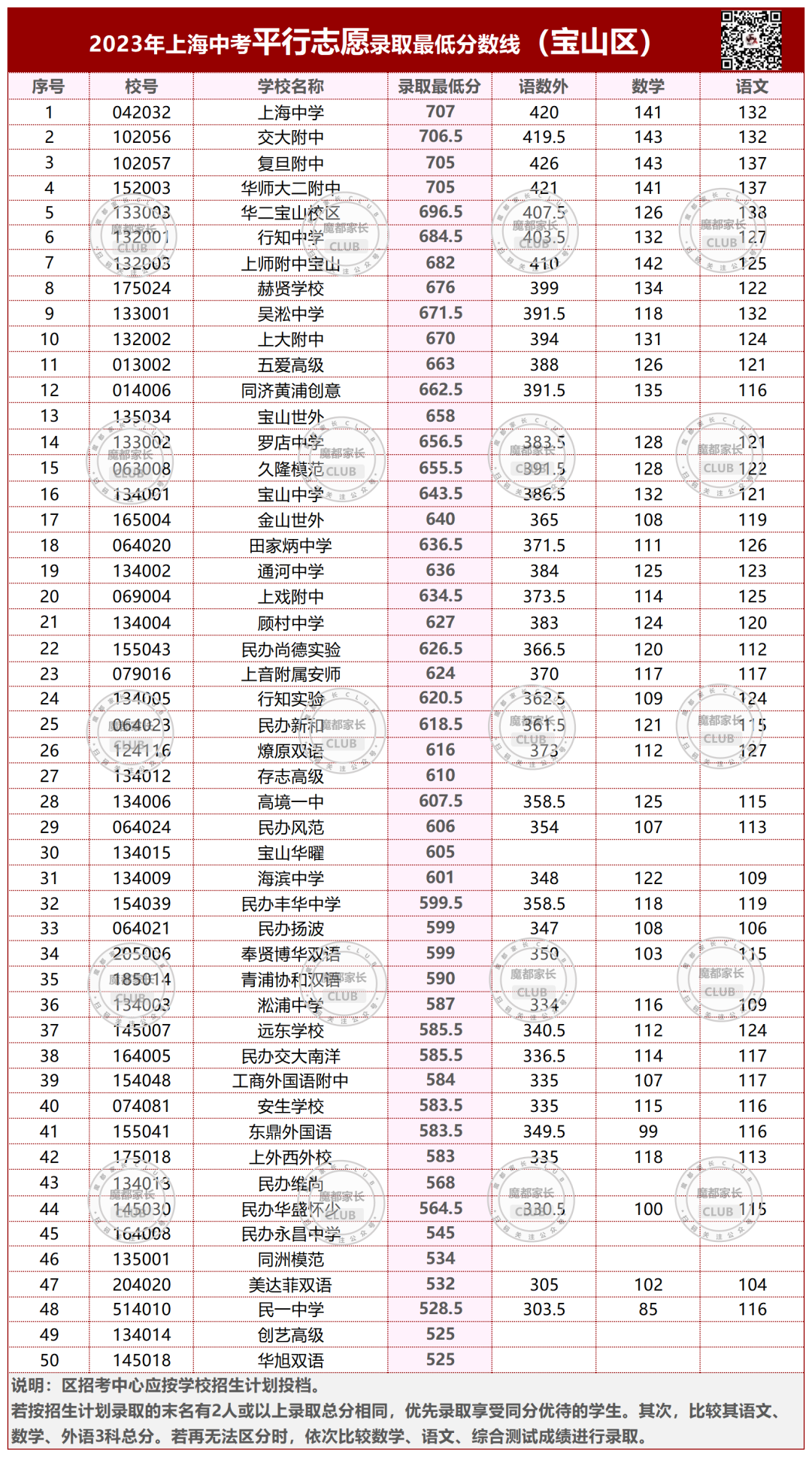
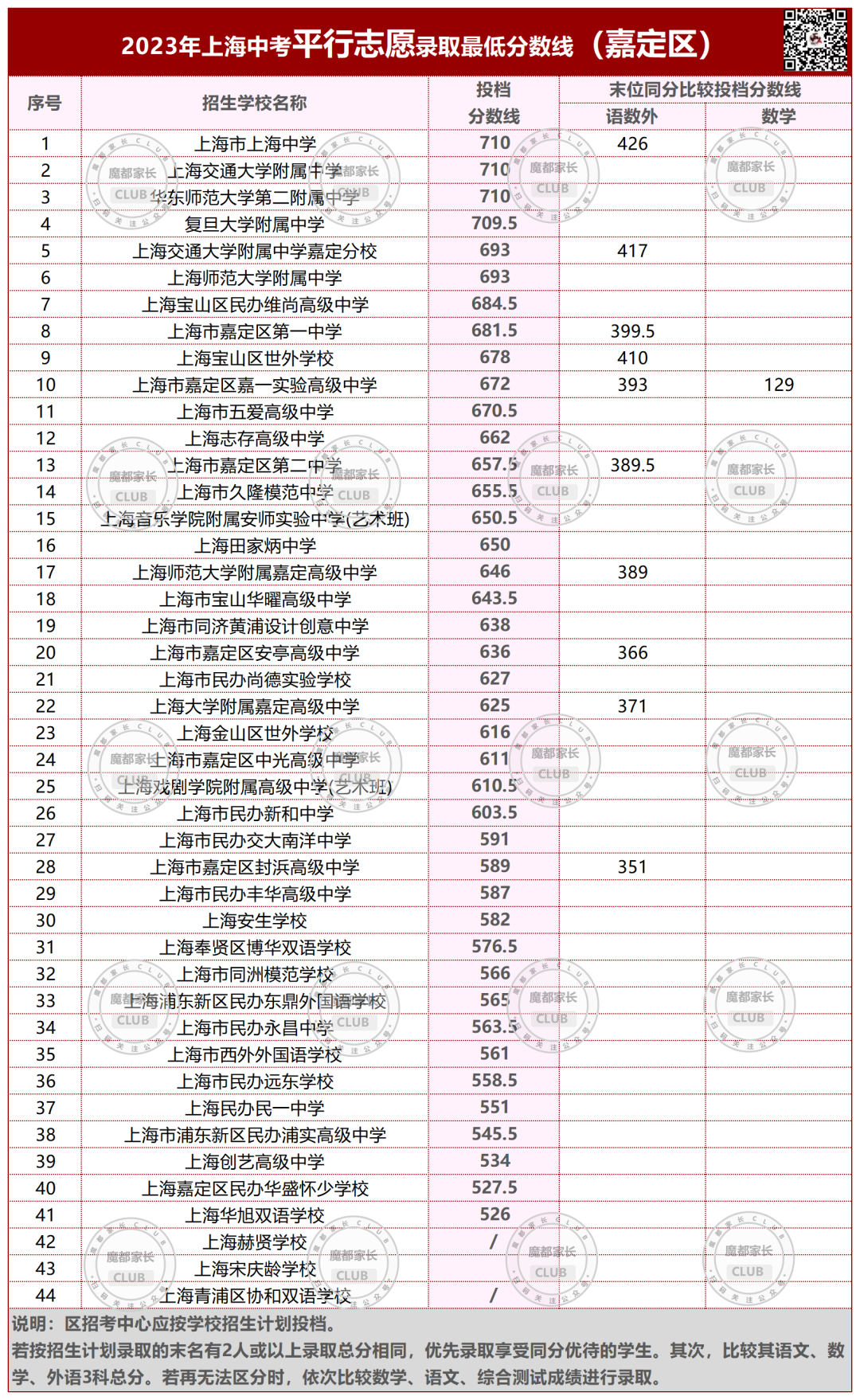
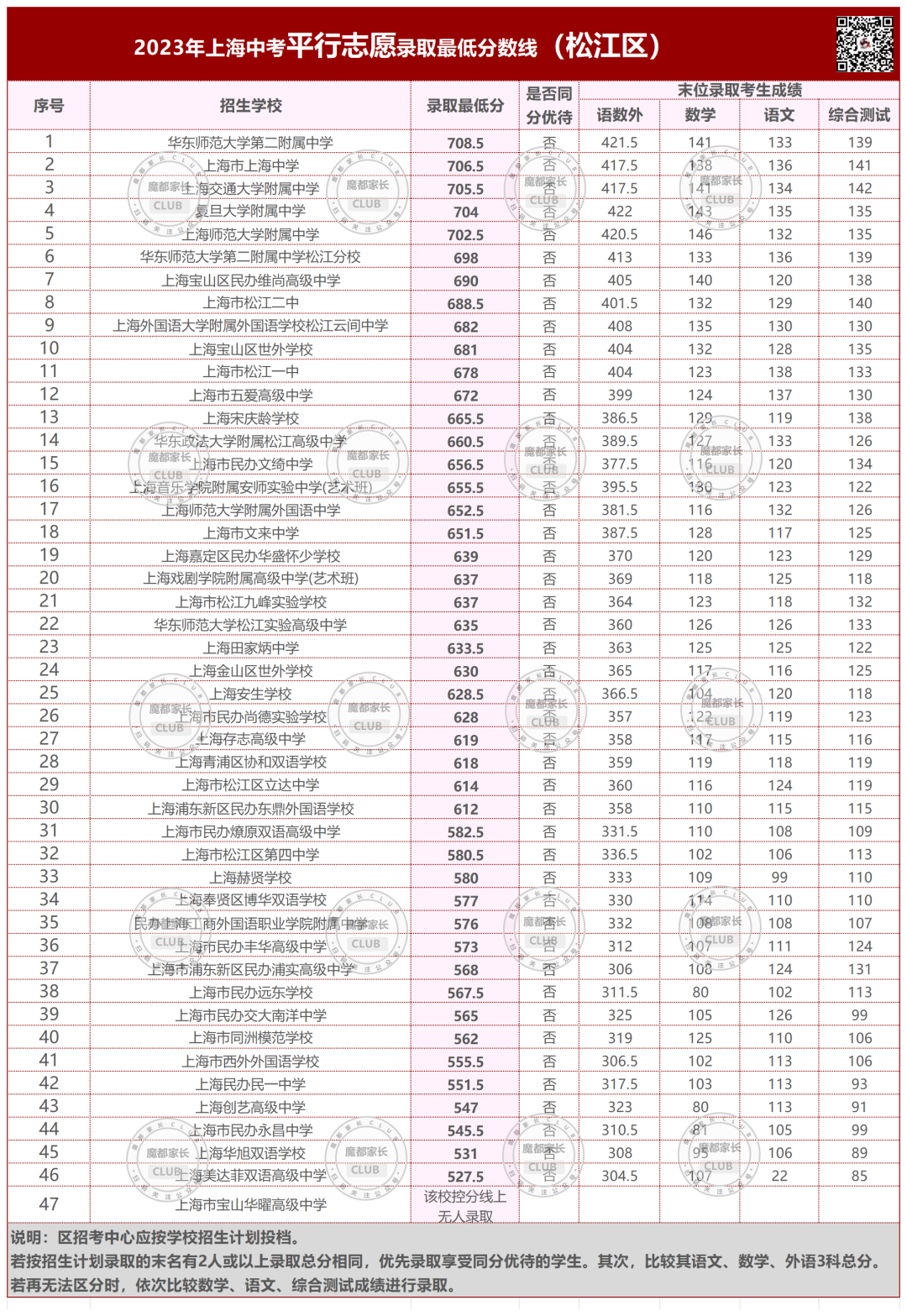
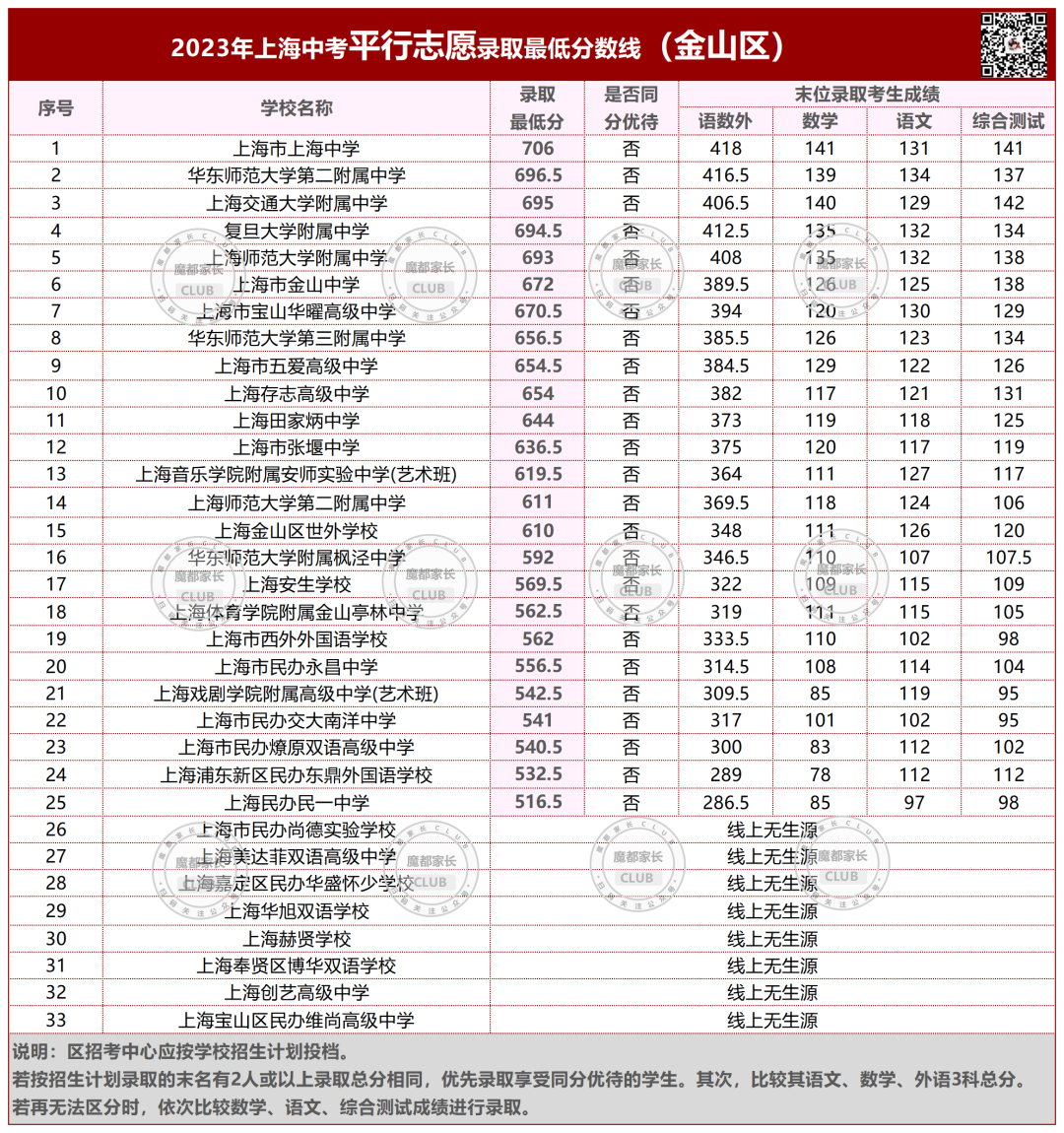
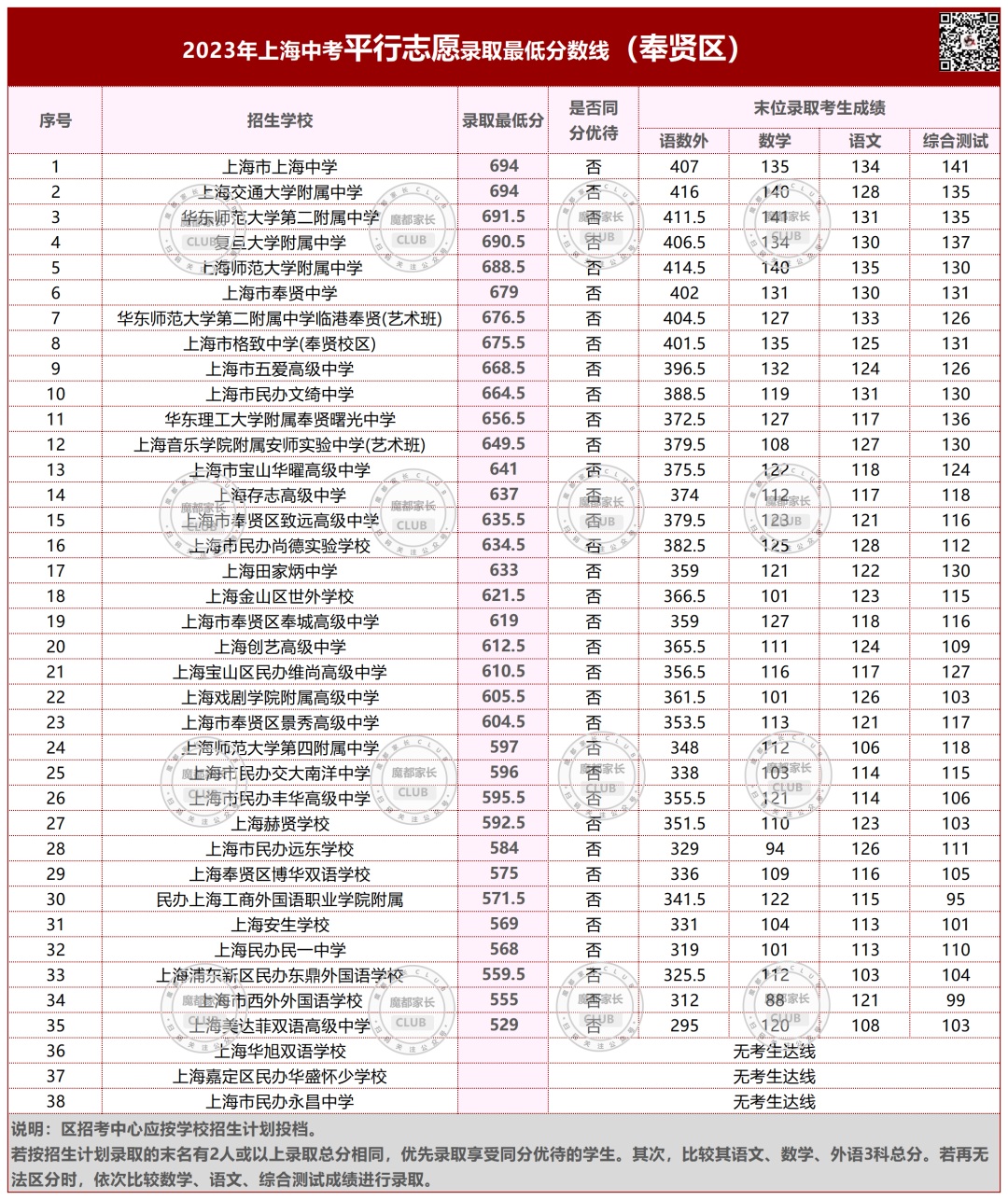
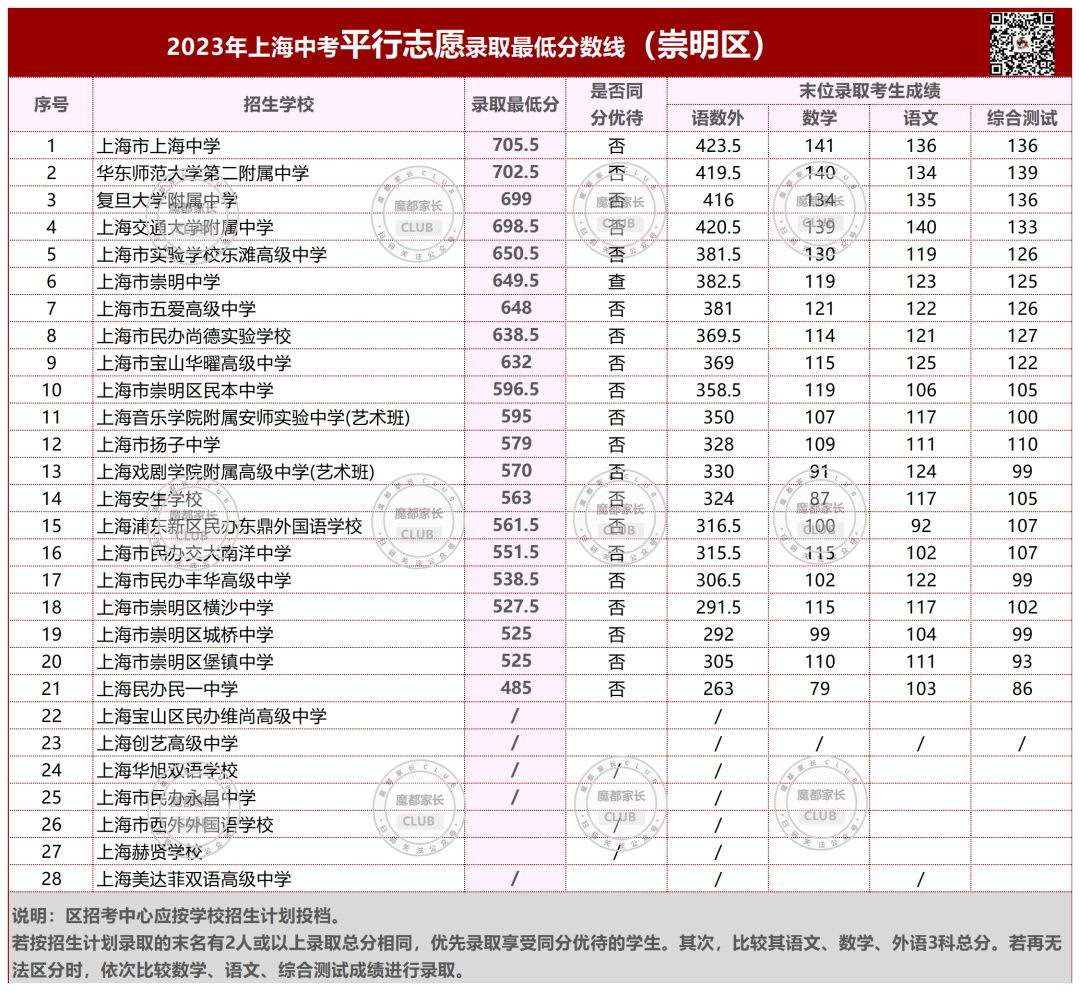
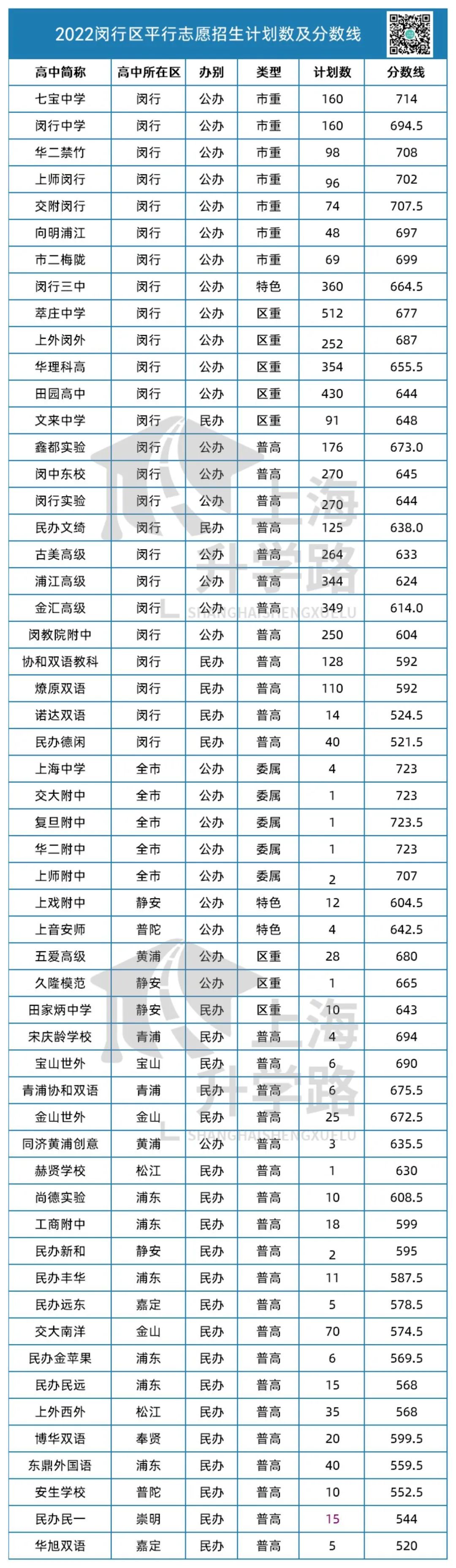
2023年,杨浦本区的平行志愿分数线。
今年杨浦区本区学校的平行志愿,均低于700分。
所有市重点都有大幅下降;640以上的区重点和特色普高下降;640以下则有不同程度上升。
民星中学,上涨62.5分;
少云中学,上涨59.5分!
放在整个上海,这种涨幅都很罕见。
杨浦区可以说是尖子生的天堂,复附、交附-清北复交、控江-985,一切都看起来那么自然,但是一旦去不了控江,就只能选择杨高、同一甚至区重点了。
但是好在杨浦区区重点很多,能够保证580左右的同学都能进区重点。
但560以下就没那么好运了,只能选择外区的高中或者民办,或者只能去三校了。
转自: https://mp.weixin.qq.com/s/kcBTeZeoVfre-EMAwPo_Vg